Colles de mathématiques
Étude avec fonctions trigonométriques réciproques
Sujet
Soit f la fonction définie sur R par
f (x) = cos(arctan(2x+1)) .
- Étudier le sens de variation de f, ses limites en ±∞ .
- Montrer que la restriction de f à [−1/2; +∞[ admet une fonction réciproque g dont on précisera l'ensemble de définition.
- Calculer f (0) puis g'(2/2) .
Corrigé de l'exercice de math
Correction
- Le sens de variation de
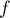 est donné par le signe de sa dérivée:
est donné par le signe de sa dérivée:
![\[f'(x)=\frac{-2}{1+(2x+1)^2}\sin(\arctan(2x+1))\]](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/2.png)
On a![$\arctan(2x+1)\in]-\pi/2,\pi/2[$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/3.png) ,
et par ailleurs
,
et par ailleurs 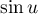 est du signe de
est du signe de 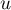 pour
pour ![$u\in]-\pi/2,\pi/2[$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/6.png) ,
,
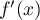 est donc du signe opposé à
est donc du signe opposé à  .
.
Mais,
![\[\arctan(2x+1)\geq 0\iff 2x+1\geq 0\iff x\geq -1/2\]](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/9.png)
Ainsi,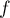 est croissante sur
est croissante sur ![$]-\infty,-1/2[$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/11.png) et décroissante sur
et décroissante sur ![$]-1/2,+\infty[$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/12.png) .
.
D'autre part, par composition des limites
![\[\begin{array}{ll}\dsp\lim_{x\to +\infty}2x+1=+\infty
&\Longrightarrow\dsp\lim_{x\to+\infty}\arctan(2x+1)=\pi/2\\[.8em]
&\Longrightarrow\dsp\lim_{x\to+\infty}\cos(\arctan(2x+1))=0\enar\]](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/13.png)
On trouve le même résultat en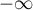 :
:
![\[\lim_{x\to-\infty}\cos(\arctan(2x+1))=\cos\lp-\dfrac\pi2\rp=0\]](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/15.png)
- D'après la première question,
on a
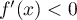 si
si 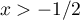 .
Ainsi,
.
Ainsi, 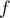 est continue et strictement décroissante sur l'intervalle
est continue et strictement décroissante sur l'intervalle
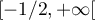 .
.
On a de plus et
et 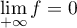 .
.
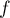 réalise donc une bijection de
réalise donc une bijection de 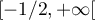 sur
sur ![$]0,1]$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/24.png) .
Elle admet en particulier une fonction réciproque
.
Elle admet en particulier une fonction réciproque  définie sur
définie sur ![$]0,1]$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/26.png) , et à valeurs dans
, et à valeurs dans 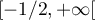 .
.
- Puisque
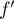 ne s'annule pas sur
ne s'annule pas sur ![$]-1/2,+\infty[$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/29.png) ,
,
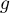 est de classe
est de classe  sur
sur ![$]0,1[$](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/32.png) .
.
En plus, en dérivant la relation, pour tout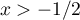 ,
,
![\[g\left( f(x)\rp=x \Longrightarrow f'(x)g'\left( f(x)\rp\]](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/34.png)
d'où,
![\[g'(f(x))=\dfrac1{f'(x)}\]](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/35.png)
Or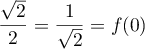 .
et donc
.
et donc
![\[g'(\sqrt 2/2)=\frac1{f'(0)}=\frac1{-1\times\sin(\pi/4)}=-\sqrt 2\]](/Generateur-Devoirs/Colles/Calcul/ex4.5_c/37.png)