Colles de mathématiques
Expression explicite d'une suite récurrente
Sujet
Soit 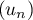 la suite définie par
la suite définie par
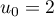 ,
,  et pour tout entier
et pour tout entier 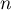 ,
,
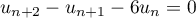 .
.
Montrer que, pour tout entier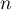 ,
,
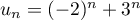 .
.
Montrer que, pour tout entier
Corrigé de l'exercice de maths: Suites - Récurrence
Correction
On peut démontrer cette formule par récurrence sur 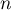 .
.
Pour ,
, 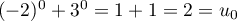 et
et 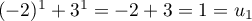 , ce qui montre que
la formule est vraie aux rangs 0 et 1.
, ce qui montre que
la formule est vraie aux rangs 0 et 1.
Soit un entier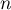 , et supposons que la formule soit vraie
aux rangs
, et supposons que la formule soit vraie
aux rangs 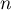 et
et 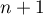 (on pourrait aussi supposer que la formule est vraie pour tout entier
(on pourrait aussi supposer que la formule est vraie pour tout entier 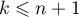 ),
c'est-à-dire que
),
c'est-à-dire que
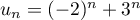 et
et
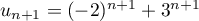 .
.
Au rang suivant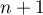 on a alors
on a alors
![\[\begin{array}{ll}u_{n+2}&=u_{n+1}+6u_n\\[.5em]
&=\lp(-2)^{n+1}+3^{n+1}\rp+6\lp(-2)^n+3^n$ \rp\\[.7em]
&=(-2)^n\lp-2+6\rp+3^n\lp3+6\rp\\[.5em]
&=(-2)^n\tm2^2+3^n\tm3^2\\[.5em]
&=(-2)^{n+2}+3^{n+2}
\enar\]](/Generateur-Devoirs/Colles/Suites/exrec_c/12.png)
et la formule est encore vraie.
On a donc montré, d'après le principe de récurrence, que pour tout entier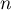 ,
,
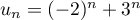 .
.
Pour
Soit un entier
Au rang suivant
![\[\begin{array}{ll}u_{n+2}&=u_{n+1}+6u_n\\[.5em]
&=\lp(-2)^{n+1}+3^{n+1}\rp+6\lp(-2)^n+3^n$ \rp\\[.7em]
&=(-2)^n\lp-2+6\rp+3^n\lp3+6\rp\\[.5em]
&=(-2)^n\tm2^2+3^n\tm3^2\\[.5em]
&=(-2)^{n+2}+3^{n+2}
\enar\]](/Generateur-Devoirs/Colles/Suites/exrec_c/12.png)
et la formule est encore vraie.
On a donc montré, d'après le principe de récurrence, que pour tout entier