🔍

Colles de mathématiques

Expression d'une série entière avec des fonctions usuelles


Sujet


On considère la série entière   ∑ n≥0 (n + 1)(n − 2)/n!xn.
Donner son rayon de convergence et l'exprimer en termes de fonctions usuelles.

Corrigé de l'exercice de maths: Séries entières

Correction


Soit $u_n=\dfrac{(n+1)(n-2)}{n!}|x|^n$, alors
\[\dfrac{u_{n+1}}{u_n}=|x|\dfrac{(n+2)(n-1)}{(n+1)^2(n-2)}\underset{+\infty}{\sim}\dfrac{|x|}{n}\to0\]

et donc, la règle de d'Alembert montre que le rayon de convergence de la série entière vaut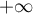 $+\infty$.

Pour exprimer la somme, la présence de $n!$ incite à se ramener à la série de l'exponentielle. Pour qu'il n'y ait finalement plus que des factorielles, on décompose le numérateur suivant
\[(n+1)(n-2)=n^2-n-2=n(n-1)-2\]

et on a donc
\[\begin{array}{lcl} \dsp\sum_{n\geq 0}\frac{(n+1)(n+2)}{n!}x^n &=&\dsp\sum_{n\geq 0}\frac{n(n-1)}{n!}x^n-2\sum_{n\geq 0}\frac{1}{n!}x^n\\ &=&\dsp\sum_{n\geq 2}\frac{1}{(n-2)!}x^n-2e^x\\ &=&\displaystyle x^2\sum_{n\geq 0}\frac{1}{n!}x^n-2e^x=(x^2-2)e^x. \enar\]