Colles de mathématiques
Expression d'une série entière avec des fonctions usuelles
Retour
Sujet
On considère la série entière
∑
n≥1
(−1)n+12nn!xn.
Donner son rayon de convergence et l'exprimer en termes de fonctions usuelles.
Donner son rayon de convergence et l'exprimer en termes de fonctions usuelles.
Corrigé de l'exercice de maths: Séries entières
Correction
Soit 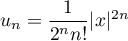 , alors, pour tout
, alors, pour tout 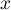 ,
,
![\[\dfrac{u_{n+1}}{u_n}=|x|^2\dfrac{1}{2(n+1)}\to0\]](/Generateur-Devoirs/Colles/SeriesEnt/exExpSE4_c/3.png)
et la règle de d'Alembert montre donc que le rayon de convergence est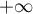 .
.
la présence de incite à se rapprocher de la série de la fonction exponentielle, ici de
incite à se rapprocher de la série de la fonction exponentielle, ici de 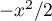 .
.
Plus précisément, en faisant attention aussi au 1er terme manquant,
![\[\begin{array}{ll}S(x)&=\dsp\sum_{n\geq 1}\frac{(-1)^{n+1}}{2^n n!}x^{2n}\\[1em]
&=-\dsp\sum_{n\geq 1}\dfrac1{n!}\lp\dfrac{-x^2}{2}\rp^n \\[1em]
&=-\dsp\sum_{n\geq 0}\dfrac1{n!}\lp\dfrac{-x^2}{2}\rp^n +1\\[1em]
&=1-\exp\lp-x^2/2\right)
\]](/Generateur-Devoirs/Colles/SeriesEnt/exExpSE4_c/7.png)
et la règle de d'Alembert montre donc que le rayon de convergence est
la présence de
Plus précisément, en faisant attention aussi au 1er terme manquant,
![\[\begin{array}{ll}S(x)&=\dsp\sum_{n\geq 1}\frac{(-1)^{n+1}}{2^n n!}x^{2n}\\[1em]
&=-\dsp\sum_{n\geq 1}\dfrac1{n!}\lp\dfrac{-x^2}{2}\rp^n \\[1em]
&=-\dsp\sum_{n\geq 0}\dfrac1{n!}\lp\dfrac{-x^2}{2}\rp^n +1\\[1em]
&=1-\exp\lp-x^2/2\right)
\]](/Generateur-Devoirs/Colles/SeriesEnt/exExpSE4_c/7.png)