🔍

Colles de mathématiques

Inégalité à démontrer


Sujet


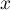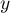Montrer que, pour tous réels $x$ et $y$ tels ques 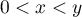$0<x<y$, on a
\[x<\dfrac{y-x}{\ln y-\ln x}<y\]


Corrigé de l'exercice de maths: Théorèmes de Rolle & accroissements finis

Correction


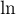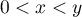La fonction $\ln$ est continue et dérivable sur $[x;y]$ pour tous couples $0<x<y$, et donc, d'après le théorème des accroissements finis, il existe $c\in]x;y[$ tel que
\[\ln y-\ln x=(y-x)\ln'(c)=(y-x)\dfrac{1}{c}\]

soit aussi
\[c=\dfrac{y-x}{\ln y-\ln x}\]

or $c\in]x;y[$, ce qui donne bien directement l'inégalité souhaitée.