Colles de mathématiques
Inégalités de convexité
Sujet
Soit ![$f:[0;1]\to\R$](/Generateur-Devoirs/Colles/Calcul/igcvx/1.png) de classe
de classe 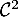 telle que
telle que 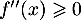 pour tout
pour tout ![$x\in[0;1]$](/Generateur-Devoirs/Colles/Calcul/igcvx/4.png) .
.
- Justifier que
 est croissante.
est croissante.
Première partie.
- Montrer que, pour tout
![$t\in[0;1]$](/Generateur-Devoirs/Colles/Calcul/igcvx/6.png) , on a
, on a
![\[f(t)\geqslant f'\lp\dfrac12\rp\lp t-\dfrac12\rp+f\lp\dfrac12\rp\]](/Generateur-Devoirs/Colles/Calcul/igcvx/7.png)
- Montrer que
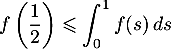 .
.
Deuxième partie.
- Montrer que, pour tout
![$t\in[0;1]$](/Generateur-Devoirs/Colles/Calcul/igcvx/9.png) , on a:
, on a:
![\[\dfrac{f(t)-f(0)}t\leqslant\dfrac{f(1)-f(t)}{1-t}\]](/Generateur-Devoirs/Colles/Calcul/igcvx/10.png)
- Montrer que
![\[\int_0^1f(s)\,ds\leqslant \dfrac{f(0)+f(1)}2\]](/Generateur-Devoirs/Colles/Calcul/igcvx/11.png)
Corrigé de l'exercice de maths: Théorèmes de Rolle & accroissements finis
Correction
Oral Ulm, 2017
- On a
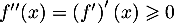 et donc
et donc 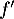 est croissante.
est croissante.
- Pour montrer cette inégalité, on peut penser à étudier le signe de la différence:
soit la fonction
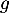 définie par l'expression
définie par l'expression
![\[g(t)=f(t)- f'\lp\dfrac12\rp\lp t-\dfrac12\rp-f\lp\dfrac12\rp\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/4.png)
Cette fonction est dérivable, avec
![\[g'(t)=f'(t)-f'\lp\dfrac12\rp\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/5.png)
Comme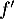 est croissante, on en déduit
que
est croissante, on en déduit
que 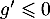 donc
donc  décroissante sur
décroissante sur ![$[0;1/2]$](/Generateur-Devoirs/Colles/Calcul/igcvx_c/9.png) et que
et que  donc
donc 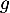 croissante sur
croissante sur ![$[1/2;1]$](/Generateur-Devoirs/Colles/Calcul/igcvx_c/12.png) .
.
En particulier,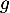 admet et atteint son minimum en
admet et atteint son minimum en 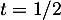 , et donc,
pour tout
, et donc,
pour tout ![$t\in[0;1]$](/Generateur-Devoirs/Colles/Calcul/igcvx_c/15.png) ,
,
![\[g(t)\geqslant g\lp\dfrac12\rp=0\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/16.png)
ce qui nous donne l'inégalité souhaitée. - On intégre la relation précédente:
![\[\int_0^1f(t)dt\geqslant f'\lp\dfrac12\rp\int_0^1\lp t-\dfrac12\rp dt+f\lp\dfrac12\rp\int_0^1dt\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/17.png)
où
![\[\int_0^1\left( t-\dfrac12\right) dt=\lb\dfrac{t^2}2-\dfrac{t}2\rb_0^1=0\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/18.png)
et
![\[\int_0^1f dt=1\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/19.png)
On obtient donc bien finalement
![\[\int_0^1f(t)dt\geqslant f\lp\dfrac12\rp\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/20.png)
- Soit
![$t\in]0;1[$](/Generateur-Devoirs/Colles/Calcul/igcvx_c/21.png) .
D'après le théorème des accroissements finis sur
.
D'après le théorème des accroissements finis sur ![$[0;t]$](/Generateur-Devoirs/Colles/Calcul/igcvx_c/22.png) , car
, car 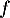 y est continue et dérivable,
y est continue et dérivable,
![\[\exists\,\alpha\in]0;t[\,;\ f(t)-f(0)=f'(\alpha)(t-0)=tf'(\alpha)\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/24.png)
De même, sur![$[t;1]$](/Generateur-Devoirs/Colles/Calcul/igcvx_c/25.png) ,
,
![\[\exists\,\beta\in]t;1[\,;\ f(1)-f(t)=f'(\beta)(1-t)\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/26.png)
Or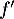 est croissante, et donc, en particulier, comme
est croissante, et donc, en particulier, comme  ,
,
![\[f'(\alpha)\leqslant f'(\beta)\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/29.png)
d'où
![\[\dfrac{f(t)-f(0)}t=f'(\alpha)\leqslant f'(\beta)=\dfrac{f(1)-f(t)}{1-t}\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/30.png)
- En isolant
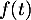 dans l'inégalité précédente, dans le but d'intégrer ensuite entre 0 et 1,
dans l'inégalité précédente, dans le but d'intégrer ensuite entre 0 et 1,
![\[\begin{array}{rl}&\dfrac{f(t)-f(0)}t\leqslant\dfrac{f(1)-f(t)}{1-t}\\[.8em]
\iff&(1-t)\left( f(t)-f(0)\rp\leqslant t\left( f(1)-f(t)\rp\\[.8em]
\iff&f(t)\leqslant tf(1)-(1-t)f(0)\enar\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/32.png)
et donc
![\[\begin{array}{lcl}\dsp\int_0^1f(t)\,dt&\leqslant&\dsp f(1)\int_0^1t\,dt-f(0)\int_0^1(1-t)\,dt\\
&=&\dfrac12f(1)+\dfrac12f(0)\enar\]](/Generateur-Devoirs/Colles/Calcul/igcvx_c/33.png)