Colles de mathématiques
Minimisation, moindres carrés et équations normales
Sujet
Soit n et p deux entiers naturels avec p≤n.
On munit Rn du produit scalaire canonique et on identifie Rn avec ℳn,1(R).
On considère une matrice A∈ℳn,p(R) de rang p et B∈ℳn,1(R).
- Démontrer qu'il existe une unique matrice X0∈ℳp,1(R) telle que
||AX0 − B|| = inf{||AX − B|| ; X∈ℳp,1(R)}
- Montrer que X0 est l'unique solution de AT AX = AT B (en notant AT la matrice transposée).
- Application : déterminer
inf{(x + y − 1)2 + (x − y)2 + (2x + y + 2)2 ; (x, y)∈R2}
Corrigé de l'exercice de maths: Espaces euclidiens
Correction
- Puisque
 est de rang
est de rang 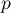 , l'application
, l'application  qui va de
qui va de 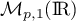 dans
dans  est injective.
est injective.
Or, est la distance
de
est la distance
de 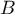 à
à 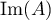 .
.
Cette distance est atteinte uniquement par le projeté orthogonal sur (qui est de dimension finie) de
(qui est de dimension finie) de 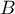 .
Ce projeté orthogonal, unique, appartenant à
.
Ce projeté orthogonal, unique, appartenant à 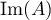 ,
s'écrit donc de façon unique
,
s'écrit donc de façon unique 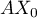 .
.
- On a
![\[\begin{array}{lcl}
AX_0=p_{\textrm{Im}(A)}(B)&\iff&
\forall Z\in \textrm{Im}(A),\ AX_0-B\perp Z\\[.4em]
&\iff& \forall X\in \mathcal{M}_{p,1}(\R),\ AX_0-B\perp AX\\[.4em]
&\iff& \forall X\in \mathcal{M}_{p,1}(\R),\ (AX)^T (AX_0-B)=0\\[.4em]
&\iff& \forall X\in\mathcal{M}_{p,1}(\R),\ X^T (A^TAX_0-A^T B)=0\\[.4em]
&\iff &A^T AX_0=A^T B
\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex6_c/13.png)
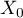 est donc bien l'unique solution de
est donc bien l'unique solution de 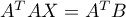 .
.
- Posons
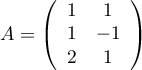 ,
et
,
et
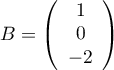 .
.
On vérifie que le rang de est
est 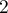 .
La borne inférieure est donc atteinte en
.
La borne inférieure est donc atteinte en  solution de
solution de
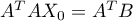 .
.
Or
![\[A^T A=\lp\begin{array}{cc} 6&2\\ 2&3 \enar\rp,\ A^TB=\lp\begin{array}{c} -3\\-1\enar\rp\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex6_c/22.png)
On vérifie que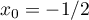 et
et 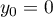 , et donc l'inf recherché vaut
, et donc l'inf recherché vaut  .
.