Colles de mathématiques
Produit scalaire avec des polynômes, matrice de Gram, et base orthonormale
Sujet
Pour P et Q deux polynômes de E = R2[X], on pose
⟨P, Q⟩ = P(0)Q(0) + P(1)Q(1) + P(2)Q(2)
- Vérifier qu'on définit ainsi un produit scalaire sur E.
- Pour des polynômes P1, P2, …, Pn,
on appelle matrice de Gram la matrice dont les coefficients
sont
⟨Pi, Pj⟩ .
Donner la matrice de Gram associée à la base canonique de E. - On pose R1(X) = X(X − 1) et
R2(X) = X(X − 2) .
Montrer que R1 et R2 sont orthgonaux.
Donner alors une base orthonormale de P.
Corrigé de l'exercice de maths: Espaces euclidiens - Polynômes - Matrices
Correction
- L'application est clairement bilinéaire, symétrique et
positive car
![\[\|P\|^2=\left( P,P\rp=\left( P(0)\rp^2+\left( P(1)\rp^2+\left( P(2)\rp^2\geqslant0\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex2_c/1.png)
Elle est de plus définie car,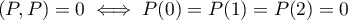 ,
et donc, en d'autres termes,
,
et donc, en d'autres termes,  admet trois racines distinctes,
ce qui est impossible pour un polynôme de degré inférieur ou égal à 2,
ormis pour le polynôme nul, soit
admet trois racines distinctes,
ce qui est impossible pour un polynôme de degré inférieur ou égal à 2,
ormis pour le polynôme nul, soit 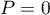 .
.
- On calcule
 .
.
-
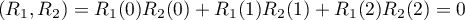 ,
et donc
,
et donc 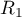 et
et 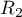 sont bien orthogonaux.
sont bien orthogonaux.
On complète avec un troisième polynôme,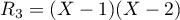 , orthogonal aux deux précédents.
, orthogonal aux deux précédents.
On normalise enfin ces trois polynômes: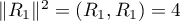 ,
,
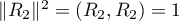 et
et 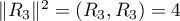 .
.
La famille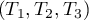 ,
avec
,
avec  ,
,
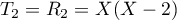 et
et 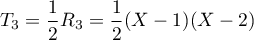 est donc une base orthonormale.
est donc une base orthonormale.