Colles de mathématiques
Signe d'une fonction dont la dérivée seconde est négative
Sujet
Soit a et b deux réels tels que
a < b .
Soit f une fonction deux fois dérivable sur [a, b]
telle que f(a)= f(b) = 0 et pour tout
x∈]a, b[,
f ''(x)≤0 .
Montrer que, pour tout x∈[a, b], f(x)≥0 .
Montrer que, pour tout x∈[a, b], f(x)≥0 .
Corrigé de l'exercice de maths: Théorèmes de Rolle & accroissements finis
Correction
Méthode 1: que des accroissements finis
Soit![$x\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/1.png) , alors le théorème des accroissements finis
sur
, alors le théorème des accroissements finis
sur ![$[a;x]$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/2.png) d'une part, puis sur
d'une part, puis sur ![$[x;b]$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/3.png) d'autre part donne
l'existence de
d'autre part donne
l'existence de
![$\alpha\in]a;x[$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/4.png) et
et
![$\beta\in]x;b[$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/5.png) et
et
![\[\begin{array}{rll}
f(x)&=f(x)-f(a)&=(x-a)f'(\alpha) \\[.6em]
-f(x)&=f(b)-f(x)&=(b-x)f'(\beta)
\enar\]](/Generateur-Devoirs/Colles/Calcul/exRAF_c/6.png)
soit
![\[f'(\alpha)=\dfrac{f(x)}{x-a} \ \text{ et }
f'(\beta)=\dfrac{-f(x)}{b-x}\]](/Generateur-Devoirs/Colles/Calcul/exRAF_c/7.png)
puis, le même théorème des accroissements finis sur![$[\alpha;\beta]$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/8.png) ,
,
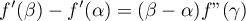
soit
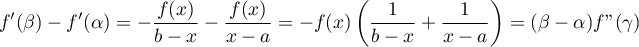
Maintenant, comme![$x\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/11.png) ,
on a
,
on a 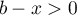 ,
, 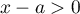 ,
et plus
,
et plus 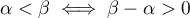 .
.
Enfin, comme , on trouve que, nécessairement,
on doit avoir
, on trouve que, nécessairement,
on doit avoir 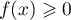 .
.
Ceci étant valable pour tout![$x\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/17.png) ,
et comme
,
et comme 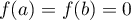 , on a bien
, on a bien
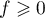 sur
sur ![$[a;b]$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/20.png) .
.
Méthode 2: Rolle et sens de variation
Comme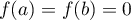 , on peut penser au théorème de Rolle:
il existe
, on peut penser au théorème de Rolle:
il existe ![$c\in]a;b[$](/Generateur-Devoirs/Colles/Calcul/exRAF_c/22.png) tel que
tel que
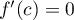 .
.
Maintenant comme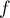 est deux fois dérivable, en
particulier
est deux fois dérivable, en
particulier 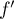 est continue, et comme
est continue, et comme  ,
on a les variations:
,
on a les variations:

d'où le signe de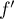 et les variations de
et les variations de  ,
,
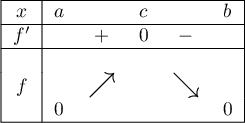
Il apparaît donc clairement que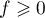 .
.
Soit
![\[\begin{array}{rll}
f(x)&=f(x)-f(a)&=(x-a)f'(\alpha) \\[.6em]
-f(x)&=f(b)-f(x)&=(b-x)f'(\beta)
\enar\]](/Generateur-Devoirs/Colles/Calcul/exRAF_c/6.png)
soit
puis, le même théorème des accroissements finis sur
soit
Maintenant, comme
Enfin, comme
Ceci étant valable pour tout
Méthode 2: Rolle et sens de variation
Comme
Maintenant comme

d'où le signe de

Il apparaît donc clairement que