Colles de mathématiques
Somme géométrique d'un endomorphisme nilpotent
Oral ESCP - filière B/L, 2021
Sujet
Oral ESCP, BL - 2021
Soit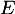 un
un 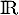 -espace vectoriel de dimension finie supérieure ou égale à 2 et soit u un endomorphisme non nul de
-espace vectoriel de dimension finie supérieure ou égale à 2 et soit u un endomorphisme non nul de 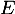 pour lequel il existe un entier naturel
pour lequel il existe un entier naturel 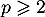 tel que
tel que 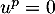 et
et 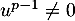 .
.
Soit
- Déterminer les valeurs propres de
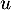 .
L'endomorphisme u est-il diagonalisable ?
.
L'endomorphisme u est-il diagonalisable ?
- Soit
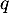 un entier vérifiant
un entier vérifiant 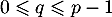 et
et 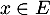 tel que
tel que 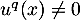 .
.
Justifier l'existence d'un tel vecteur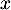 .
Montrer que la famille
.
Montrer que la famille 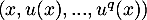 est une famille libre de
est une famille libre de 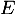 .
.
- On note
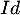 l'endomorphisme identité de
l'endomorphisme identité de 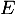 et soit
et soit  l'endomorphisme de
l'endomorphisme de 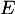 défini par:
défini par:
![\[v = Id + u + \dfrac{u^2}{2!} + \dots + \dfrac{u^{p-1}}{(p-1)!}\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1/19.png)
Montrer que est bijectif.
est bijectif.
- Déterminer un lien entre
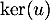 et
et 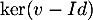 .
.
- En déduire les valeurs propres de
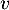 .
L'endomorphisme
.
L'endomorphisme 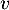 est-il diagonalisable ?
est-il diagonalisable ?
Corrigé de l'exercice de maths: Diagonalisation - Annales ESCP - B/L
Correction
Oral ESCP, BL - 2021
- Soit
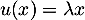 , avec
, avec 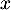 non nul, alors, en appliquant
non nul, alors, en appliquant 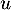 on a
on a  , puis, en réitérant,
, puis, en réitérant, 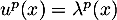 .
Or, par définition,
.
Or, par définition,  , d'où nécessairement
, d'où nécessairement 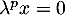 , et comme
, et comme  non nul, on en déduit que
non nul, on en déduit que 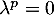 c'est-à-dire que
c'est-à-dire que  .
.
La seule valeur propre possible de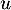 est donc 0.
est donc 0.
Maintenant si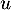 était diagonalisable,
était diagonalisable,  serait semblable (ou sa matrice) à l'endomorphisme nul (ou la matrice nulle), et donc
serait semblable (ou sa matrice) à l'endomorphisme nul (ou la matrice nulle), et donc 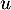 serait nul, ce qui est impossible par hypothèse.
serait nul, ce qui est impossible par hypothèse.
Ainsi,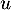 n'est pas diagonalisable.
n'est pas diagonalisable.
- Supposons que pour tout entier
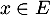 on ait
on ait 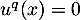 , c'est-à-dire
, c'est-à-dire 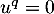 , alors si
, alors si 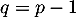 c'est contraire à la définition de
c'est contraire à la définition de 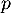 car
car 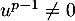 ,
si
,
si 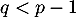 , en appliquant
, en appliquant 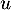
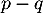 fois on obtiendrait
fois on obtiendrait 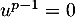 ce qui est de même absurde.
ce qui est de même absurde.
En résumé, il existe nécessairement un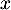 tel que
tel que 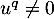 .
.
Soit alors ,
, 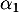 , …,
, …, 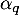 des réels tels que
des réels tels que
![\[\alpha_0x+\alpha_1u(x)+\dots+\alpha_qu^q(x)=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/31.png)
En appliquant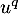 tous les termes s'annulent sauf le premier et on obtient alors
tous les termes s'annulent sauf le premier et on obtient alors
![\[\alpha_0u^q(x)=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/33.png)
et donc, comme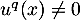 , on en tire que
, on en tire que 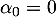 .
.
En appliquant de même alors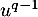 à la relation, on obtient de même que
à la relation, on obtient de même que 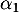 et ainsi de suite pour tous les coefficients
et ainsi de suite pour tous les coefficients 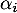 .
.
On trouve ainsi que et donc que cette famaille est libre.
et donc que cette famaille est libre.
- On peut d'intéresser au noyau de
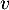 . Soit
. Soit 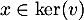 , alors
, alors
![\[v(x)=x+u(x)+\dots\dfrac{u^{p-1}(x)}{(p-1)!}=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/42.png)
On se ramène alors alors à la question précédente: soit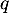 le plus grand entier tel que
le plus grand entier tel que 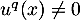 , ce qui permet de tronquer la relation précédente en
, ce qui permet de tronquer la relation précédente en
![\[v(x)=x+u(x)+\dots\dfrac{u^q(x)}{q!}=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/45.png)
Maintenant, comme à la question précédente, en appliquant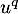 , tous les termes sauf le premier s'annulent, et on obtient
, tous les termes sauf le premier s'annulent, et on obtient
![\[u^q(x)=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/47.png)
et donc nécessairement, par définition de l'entier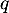 , on obtient
, on obtient 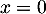 .
.
On a donc trouvé que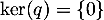 et donc que
et donc que 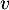 est inversible.
est inversible.
- On a
![\[v-Id=u\left( Id+\dfrac{u}2+\dots+\dfrac{u^{p-2}}{(p-1)!}\rp\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/52.png)
et donc si alors aussi
alors aussi 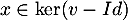 , d'où
, d'où
![\[\ker(u)\subset\ker(v-Id)\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/55.png)
Réciproquement, soit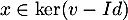 , c'est-à-dire que
, c'est-à-dire que
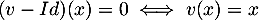 et donc
et donc
![\[u(x)+\dfrac{u^2(x)}{2!}+\dots+\dfrac{u^{p-1}(x)}{(p-1)!}=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/58.png)
Soit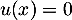 , soit on peut, à nouveau, définir
, soit on peut, à nouveau, définir 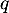 le plus petit entier tel que
le plus petit entier tel que 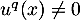 , en appliquant
, en appliquant 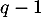 fois l'endomorphisme
fois l'endomorphisme 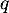 , tous les termes sauf le premier s'annulent et on obtient
, tous les termes sauf le premier s'annulent et on obtient
![\[u^q(x)\not=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/64.png)
ce qui est alors absurde. On en déduit que nécessairement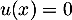 et donc que
et donc que
![\[\ker(v-Id)\subset\ker(u)\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/66.png)
Finalement, on a bien montré que
![\[\ker(v-Id)=\ker(u)\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/67.png)
- Soit
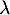 une éventuelle valeur propre de
une éventuelle valeur propre de 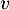 , c'est-à-dire que
, c'est-à-dire que
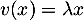 et donc, d'après la définition de
et donc, d'après la définition de 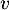 ,
,
![\[(1-\lambda)x+u(x)+\dots+\dfrac{u^{p-1}(x)}{(p-1)!}=0\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1_c/72.png)
Si , alors avec le même raisonnement qu'utilisé (plusieurs fois) précédemment on obtient une contradiction sur la liberté de la famille
, alors avec le même raisonnement qu'utilisé (plusieurs fois) précédemment on obtient une contradiction sur la liberté de la famille  .
.
La seule valeur propre possible est donc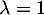 , et donc
, et donc 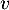 ne peut pas être diagonalisable car si
ne peut pas être diagonalisable car si 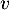 l'était, il serait semblable à l'identité, donc égal à l'identité, et donc
l'était, il serait semblable à l'identité, donc égal à l'identité, et donc 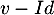 serait nul tout comme
serait nul tout comme 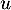 car alors on aurait
car alors on aurait
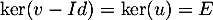 .
.