Colles de mathématiques
Somme géométrique d'un endomorphisme nilpotent
Oral ESCP - filière B/L, 2021
Exercice de maths: Diagonalisation - Annales ESCP - B/L
Sujet
Oral ESCP, BL - 2021
Soit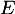 un
un 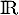 -espace vectoriel de dimension finie supérieure ou égale à 2 et soit u un endomorphisme non nul de
-espace vectoriel de dimension finie supérieure ou égale à 2 et soit u un endomorphisme non nul de 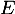 pour lequel il existe un entier naturel
pour lequel il existe un entier naturel 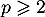 tel que
tel que 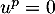 et
et 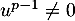 .
.
Soit
- Déterminer les valeurs propres de
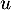 .
L'endomorphisme u est-il diagonalisable ?
.
L'endomorphisme u est-il diagonalisable ?
- Soit
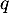 un entier vérifiant
un entier vérifiant 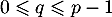 et
et 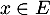 tel que
tel que 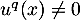 .
.
Justifier l'existence d'un tel vecteur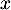 .
Montrer que la famille
.
Montrer que la famille 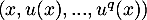 est une famille libre de
est une famille libre de 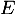 .
.
- On note
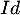 l'endomorphisme identité de
l'endomorphisme identité de 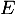 et soit
et soit  l'endomorphisme de
l'endomorphisme de 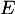 défini par:
défini par:
![\[v = Id + u + \dfrac{u^2}{2!} + \dots + \dfrac{u^{p-1}}{(p-1)!}\]](/Generateur-Devoirs/Colles/Diagonalisation/ESCP-BL-2021-4.1/19.png)
Montrer que est bijectif.
est bijectif.
- Déterminer un lien entre
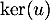 et
et 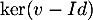 .
.
- En déduire les valeurs propres de
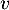 .
L'endomorphisme
.
L'endomorphisme 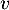 est-il diagonalisable ?
est-il diagonalisable ?