Colles de mathématiques
Sous-espaces vectoriels supplémentaires
Sujet
Soit
F et G les ensembles
F =
{(a, a, a) ∈ R3 ;
a∈R}
et
G = {(b+c, b, c) ∈ R3 ;
b∈R ,
c∈R}
.
- Montrer que F et G sont des sous-espaces vectoriels de R3.
- Déterminer F∩G.
- F et G sont-ils supplémentaires ?
Corrigé de l'exercice de maths: Espaces vectoriels
Correction
- Si
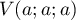 et
et 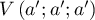 alors
alors
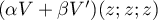 avec
avec 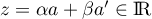 ,
c'est-à-dire
,
c'est-à-dire 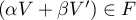 .
.
De même, si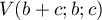 et
et 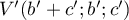 alors
alors
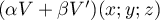 avec
avec
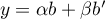 et
et 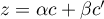 et
et 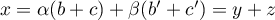 .
.
- Soit
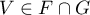 ,
donc
,
donc 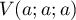 et
et 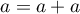 , ainsi
, ainsi  et
et 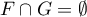 .
.
- On peut raisonner avec des bases de
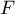 et
et 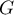 :
:
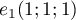 est une base de
est une base de 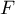 ,
et
,
et 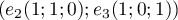 en est une pour
en est une pour 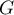 .
.
On remarque (et montre) que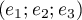 est une base de
est une base de 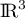 ,
ce qui montre que
,
ce qui montre que 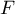 et
et 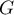 sont supplémentaires.
sont supplémentaires.