Colles de mathématiques
Suite implicite: racine d'une suite de fonctions
Sujet
Pour tout  on pose
on pose 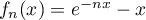 .
.
- Montrer que l'équation
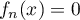 admet une unique solution positive. On la notera
admet une unique solution positive. On la notera 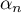 .
.
- Montrer que pour tout entier
 et tout réel
et tout réel 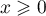 on a
on a 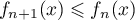 .
.
- En déduire que la suite
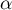 est décroissante.
est décroissante.
- Monter qu'elle converge vers une limite
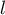 .
.
- Montrer que
 n'est pas strictement positive. Donner alors la valeur de
n'est pas strictement positive. Donner alors la valeur de 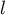 .
.
- Montrer que
 .
.
Corrigé de l'exercice de maths: Suites - Limite
Correction
-
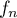 est dérivable sur
est dérivable sur  avec pour tout réel
avec pour tout réel 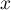 ,
, 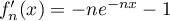 .
Or
.
Or 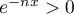 et donc
et donc 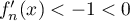 d'où
d'où  est strictement décroissante sur
est strictement décroissante sur 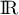 et donc aussi sur
et donc aussi sur  .
.
De plus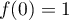 et
et  ;
ainsi
;
ainsi 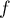 est une bijection de
est une bijection de 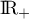 sur
sur ![$]-\infty;1]$](/Generateur-Devoirs/Colles/Suites/exSuiteImplicite_c/14.png) .
En particulier, il existe un unique réel
.
En particulier, il existe un unique réel ![$\alpha_n\in]-\infty;1]$](/Generateur-Devoirs/Colles/Suites/exSuiteImplicite_c/15.png) tel que
tel que 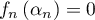 .
.
- Pour tout
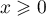 , on a
, on a
![\[\begin{array}{ll} f_{n+1}(x)-f_n(x)
&=\left( e^{-(n+1)x}-x\rp-\left( e^{-nx}-x\rp\\[.6em]
&=e^{-nx}\left( e^{-x}-1\rp\enar\]](/Generateur-Devoirs/Colles/Suites/exSuiteImplicite_c/18.png)
Or, pour tout réel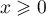 ,
,  et
et  ,
d'où
,
d'où
![\[f_{n+1}(x)-f_n(x)\leqslant0\iff f_{n+1}(x)\leqslant f_n(x)\]](/Generateur-Devoirs/Colles/Suites/exSuiteImplicite_c/22.png)
- On a donc, pout tout
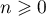 ,
,
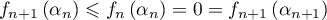 .
.
Comme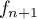 est décroissante on obtient donc
est décroissante on obtient donc
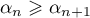 ,
ce qui montre que la suite
,
ce qui montre que la suite 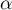 est décroissante.
est décroissante.
- La suite
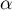 est une suite de nombres positifs, donc minorée par
est une suite de nombres positifs, donc minorée par  .
Elle est de plus décroissante.
On en déduit qu'elle converge vers une limite
.
Elle est de plus décroissante.
On en déduit qu'elle converge vers une limite 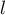 .
.
- Supposons
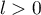
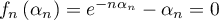 , et on donc
, et on donc
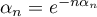 .
.
Si , on a alors
, on a alors 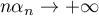 et alors
et alors 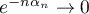 , ce qui est contradictoire
avec
, ce qui est contradictoire
avec 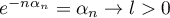 .
.
Ainsi,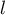 ne peut pas être strictement positif.
ne peut pas être strictement positif.
Comme , on a nécessairement par ailleurs
, on a nécessairement par ailleurs 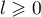 .
.
On en déduit que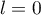 .
.
- Comme précédemment, on a
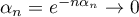 .
.
Ainsi,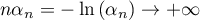 .
.