Colles de mathématiques
Suite récurrente avec une racine carrée
Sujet
Soit  et
et 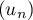 la suite définie par récurrence par
la suite définie par récurrence par 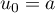 et
et
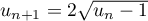 pour
pour 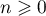 .
.
- Soit
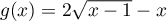 pour
pour 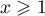 .
Étudier le signe de
.
Étudier le signe de  .
.
- Étudier la convergence de la suite
 .
.
- On pose
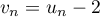 . Montrer que
. Montrer que
![\[\dfrac1{v_{n+1}}-\dfrac1{v_n}\underset{n\to+\infty}{\longrightarrow}\dfrac14\]](/Generateur-Devoirs/Colles/Suites/SR-racine/11.png)
Corrigé de l'exercice de maths: Suites
Correction
- On peut par exemple chercher à résoudre l'inéquation
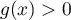 pour
pour 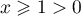 :
:
![\[\begin{array}{ll}g(x)>0&\iff2\sqrt{x-1}>x \\[.6em]
&\iff4(x-1)>x^2\\[.6em]
&\iff x^2-4x+4=(x-2)^2<0\enar\]](/Generateur-Devoirs/Colles/Suites/SR-racine_c/3.png)
Cette inéquation n'a aucune solution, ce qui montre que pour tout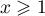 , on a
, on a 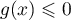 , et que
, et que 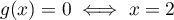 .
.
- D'après ce qui précède, on a, si
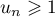 ,
,
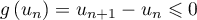 ,
soit
,
soit 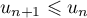 et donc
et donc 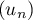 décroissante.
décroissante.
Il reste à montrer qu'on a bien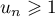 pour tout entier
pour tout entier 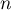 .
.
En fait, on a et donc
et donc 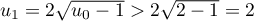 .
.
Cette initialisation nous incite à montrer plutôt que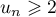 :
:
C'est donc vrai pour et
et  , puis, si c'est vrai à rang
, puis, si c'est vrai à rang 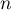 ,
c'est-à-dire
,
c'est-à-dire 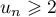 ,
alors
,
alors
![\[u_{n+1}=2\sqrt{u_n-1}\geqslant2\sqrt{2-1}=2\]](/Generateur-Devoirs/Colles/Suites/SR-racine_c/20.png)
et cette propriété est donc héréditaire.
Le principe de récurrence nous permet alors de conclure que pour tout entier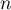 ,
, 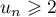 et donc aussi que
et donc aussi que 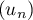 est décroissante.
est décroissante.
Cett suite est donc maintenant décroissante et minorée par 2, et elle converge donc vers une limite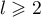 qui est nécessairement un point fixe
de
qui est nécessairement un point fixe
de 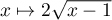 ou encore une solution de l'équation
ou encore une solution de l'équation 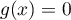 .
.
On a vu que cela ne peut être que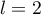 .
.
-
![\[\begin{array}{ll}\dfrac1{v_{n+1}}-\dfrac1{v_n}
&=\dfrac1{u_{n+1}-2}-\dfrac1{u_n-2}\\[1.2em]
&=\dfrac1{2\sqrt{u_n-1}-2}-\dfrac1{u_n-2}\\[1.2em]
&=\dfrac{2\sqrt{u_n-1}+2}{4\left( u_n-1\rp-4}-\dfrac1{u_n-2}\\[1.2em]
&=\dfrac{2\sqrt{u_n-1}-2}{4\left( u_n-2\right)}\\[1.2em]
&=\dfrac{\sqrt{u_n-1}-1}{2\left( u_n-2\right)}
\enar\]](/Generateur-Devoirs/Colles/Suites/SR-racine_c/28.png)
On peut alors penser à mulitplier par la quantité conjuguée
![\[\begin{array}{ll}\dfrac1{v_{n+1}}-\dfrac1{v_n}
&=\dfrac{\sqrt{u_n-1}-1}{2\left( u_n-2\right)}\tm\dfrac{\sqrt{u_n-1}+1}{\sqrt{u_n-1}+1}\\
&=\dfrac{\left( u_n-1\rp-1}{2\left( u_n-2\rp\left(\sqrt{u_n-1}+1\rp}\\
&=\dfrac{u_n-2}{2\left( u_n-2\rp\left(\sqrt{u_n-1}+1\rp}\\
&=\dfrac1{2\lp\sqrt{u_n-1}+1\right)}\enar\]](/Generateur-Devoirs/Colles/Suites/SR-racine_c/29.png)
et donc, comme on a a vu que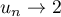 , on trouve donc que
, on trouve donc que
![\[\lim_{n\to+\infty}\dfrac1{v_{n+1}}-\dfrac1{v_n}=\dfrac14\]](/Generateur-Devoirs/Colles/Suites/SR-racine_c/31.png)
On peut aussi utiliser un développement limité, en revenant d'abord à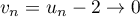 , puis
, puis
![\[\begin{array}{ll}\dfrac1{v_{n+1}}-\dfrac1{v_n}
&=\dfrac{\sqrt{1+v_n}-1}{2v_n}\\[1.2em]
&=\dfrac{1+\frac12v_n+O\left( v_n^2\rp-1}{2v_n}\\[1.2em]
&=\dfrac14+O\left( v_n\rp\underset{n\to+\infty}{\longrightarrow}\dfrac14\enar\]](/Generateur-Devoirs/Colles/Suites/SR-racine_c/33.png)