Colles de mathématiques
Suites récurrentes couplées
Sujet
Soit 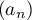 ,
,  et
et 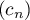 trois suites réelles telles que
trois suites réelles telles que
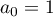 ,
, 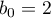 ,
, 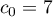 , et vérifiant les relations de récurrence :
, et vérifiant les relations de récurrence :


- On considère le vecteur colonne
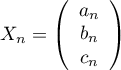 .
Trouver une matrice
.
Trouver une matrice 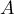 telle que
telle que 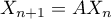 .
.
- Soit
 .
Calculer
.
Calculer 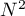 ,
, 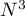 , puis
, puis  pour
pour 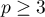 .
.
- Montrer que
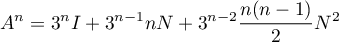 .
.
En déduire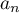 ,
,  et
et 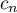 en fonction de
en fonction de 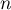 .
.
Corrigé de l'exercice de maths: Suites - Matrices
Correction
- Soit
 ,
alors
,
alors 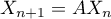 .
.
- On a :
 , et
, et
 .
.
Pour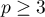 , on a alors
, on a alors 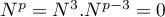 .
.
- On a
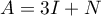 et, comme les matrices
et, comme les matrices 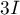 et
et 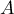 commutent
(
commutent
(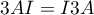 ), on peut utiliser le binôme de Newton qui fournit
directement le résultat demandé.
), on peut utiliser le binôme de Newton qui fournit
directement le résultat demandé.
- On a donc
 .
.
On obtient alors :