Colles de mathématiques
Calcul de limite avec équivalents
Retour
Sujet
Étudier la limite de la suite 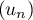 définie par,
pour tout entier
définie par,
pour tout entier 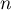 ,
,
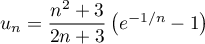
Corrigé de l'exercice de maths: Suites - Limite - Équivalents - Développements limités
Correction
On utilise l'équivalent 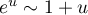 lorsque
lorsque 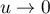 .
.
Ici, et donc
et donc  ,
et alors,
,
et alors,
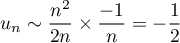 .
.
On trouve donc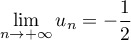
Ici,
On trouve donc