Colles de mathématiques
Calcul matriciel - Puissance n-ième
Sujet
Soit  et
et 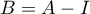 .
.
Calculer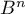 pour tout
pour tout 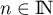 .
En déduire
.
En déduire  .
.
 et
et Calculer
Corrigé de l'exercice de maths: Matrices
Correction
 ,
,
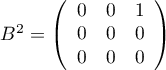 ,
,
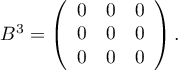 .
.
On en déduit alors que, pour tout
On a alors
![\[A^n=\sum_{k=0}^n\binom{n}{k}I^{n-k}B^k
=I^{n}+\binom{n}{1}I^{n-1}B+\binom{n}{2}I^{n-2}B^2\]](/Generateur-Devoirs/Colles/matrices/ex3_c/10.png)
soit
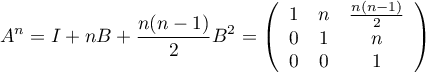 .
.