Colles de mathématiques
Cauchy-Schwarz et une application (bis)
Sujet
Montrer que pour tous réels,
a1, a2, a3, et a4 on a
| a1 + a2 + a3 + a4| ≤a12 + a22 + a32 + a42
Corrigé de l'exercice de maths: Produit scalaire dans Rn - Espaces euclidiens
Correction
L'inégalité de inégalité de Cauchy-Schwarz s'écrit
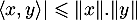 .
.
Dans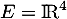 avec le produit scalaire canonique,
et
avec le produit scalaire canonique,
et
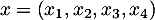 et
et
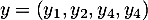 ,
cette inégalité s'écrit donc
,
cette inégalité s'écrit donc
![\[\left|\sum_{i=1}^4x_iy_i\right|\leqslant
\sqrt{\sum_{i=1}^4x_i^2}
\sqrt{\sum_{i=1}^4y_i^2}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS2_c/5.png)
Maintenant, avec le vecteur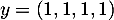 , on obtient
, on obtient
![\[\left|\sum_{i=1}^4x_i\right|\leqslant
\sqrt{\sum_{i=1}^4x_i^2}
\sqrt{\sum_{i=1}^41}
\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS2_c/7.png)
ce qui, avec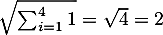 , est l'inégalité recherchée.
, est l'inégalité recherchée.
Dans
![\[\left|\sum_{i=1}^4x_iy_i\right|\leqslant
\sqrt{\sum_{i=1}^4x_i^2}
\sqrt{\sum_{i=1}^4y_i^2}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS2_c/5.png)
Maintenant, avec le vecteur
![\[\left|\sum_{i=1}^4x_i\right|\leqslant
\sqrt{\sum_{i=1}^4x_i^2}
\sqrt{\sum_{i=1}^41}
\]](/Generateur-Devoirs/Colles/EspaceEuclidien/CS2_c/7.png)
ce qui, avec