Colles de mathématiques
Convergence de la série exponentielle (avec des suites adjacentes)
Sujet
Soit la suite 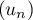 définie par
définie par
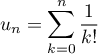 .
On souhaite montrer que
.
On souhaite montrer que 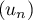 est une suite convergente.
est une suite convergente.
On pose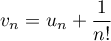 .
.
Montrer que ces suites sont adjacentes et conclure.
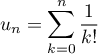 .
On souhaite montrer que
.
On souhaite montrer que On pose
Montrer que ces suites sont adjacentes et conclure.
Corrigé de l'exercice de maths: Suites - Sommes - Limite
Correction
On a directement
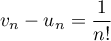 ce qui montre que
ce qui montre que
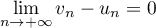 .
.
Par ailleurs, d'une part,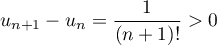 et donc
et donc  est croissante.
est croissante.
D'autre part,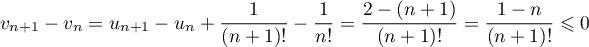 pour
pour  ,
ce qui montre que
,
ce qui montre que 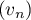 est décroissante.
est décroissante.
Ce qui précède montre que les suites et
et 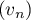 sont adjacentes et convergent donc
vers la même limite
sont adjacentes et convergent donc
vers la même limite 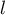 .
.
Ainsi, en particulier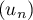 est convergente.
est convergente.
Par ailleurs, d'une part,
D'autre part,
Ce qui précède montre que les suites
Ainsi, en particulier