Colles de mathématiques
Convergence de Série harmonique alternée
Sujet
On considère la suite 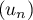 définie par la somme
définie par la somme
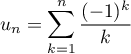 .
.
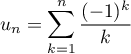 .
.
- En calculant les premiers termes de cette suite, montrer qu'elle n'est pas monotone.
- On pose
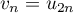 et
et 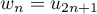 ,
Montrer que ces suites sont adjacentes.
Que peut-on en conclure ?
,
Montrer que ces suites sont adjacentes.
Que peut-on en conclure ?
Corrigé de l'exercice de maths: Suites - Sommes
Correction
- On a
 ,
, 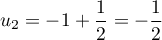 et
et 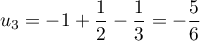 .
.
Ainsi,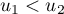 mais
mais 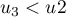 .
La suite n'est pas ni croissante, ni décroissante.
.
La suite n'est pas ni croissante, ni décroissante.
-
![\[\begin{array}{ll}
v_{n+1}-v_n&=u_{2(n+1)}-u_{2n}\\[.8em]
&=\dsp\sum_{k=1}^{2n+2}\dfrac{(-1)^k}{k}
-\sum_{k=1}^{2n}\dfrac{(-1)^k}{k} \\[2em]
&=\dfrac{(-1)^{2n+2}}{2n+2}+\dfrac{(-1)^{2n+1}}{2n+1} \\[1em]
&=\dfrac{1}{2n+2}+\dfrac{-1}{2n+1}
=\dfrac{-1}{(2n+2)(2n+1)}<0
\enar\]](/Generateur-Devoirs/Colles/Suites/ex16_c/6.png)
ce qui montre que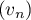 est décroissante.
est décroissante.
De même,
![\[\begin{array}{ll}
w_{n+1}-w_n&=u_{2(n+1)+1}-u_{2n+1}=u_{2n+3}-u_{2n+1}\\[.8em]
&=\dsp\sum_{k=1}^{2n+3}\dfrac{(-1)^k}{k}
-\sum_{k=1}^{2n+1}\dfrac{(-1)^k}{k} \\[2em]
&=\dfrac{(-1)^{2n+3}}{2n+3}+\dfrac{(-1)^{2n+2}}{2n+2} \\[1em]
&=\dfrac{-1}{2n+3}+\dfrac{1}{2n+2}
=\dfrac{1}{(2n+3)(2n+2)}>0
\enar\]](/Generateur-Devoirs/Colles/Suites/ex16_c/8.png)
ce qui montre que la suite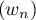 est croissante.
est croissante.
Enfin,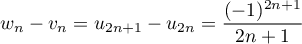 et donc,
et donc, 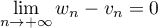 .
.
On déduit des trois résultats prcédents que et
et 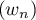 sont adjacentes et que,
en particulier ces deux suites sont convergentes vers la même limite
sont adjacentes et que,
en particulier ces deux suites sont convergentes vers la même limite 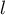 .
.
De plus, comme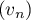 et
et 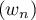 sont les deux sous-suites
extraites de
sont les deux sous-suites
extraites de 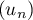 de rangs respectivement pairs et impairs,
on en déduit que
de rangs respectivement pairs et impairs,
on en déduit que 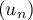 converge aussi vers la même limite.
converge aussi vers la même limite.