Colles de mathématiques
Covariance d'un couple
Sujet
Soit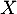 
une variable aléatoire dont la loi de probabilité est donnée par
![\[P(X=-1)=P(X=0)=P(X=1)=\dfrac13\]](/Generateur-Devoirs/Colles/CVA/covariance-1/2.png)
et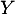
une variable aléatoire telle que
![\[Y=\la\begin{array}{lll}0&\text{si}&X\not=0\\1&\text{si}&X=0\enar\right.\]](/Generateur-Devoirs/Colles/CVA/covariance-1/4.png)
Calculer la covariance de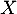
et 
.
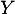Les variables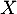
et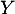 
sont-elles indépendantes ?
une variable aléatoire dont la loi de probabilité est donnée par
et
une variable aléatoire telle que
Calculer la covariance de
et .
Les variables
et sont-elles indépendantes ?
Corrigé de l'exercice de maths: Couples de variables aléatoires
Correction
On a
![\[cov(X,Y)=E(XY)-E(X)E(Y)\]](/Generateur-Devoirs/Colles/CVA/covariance-1_c/1.png)
On a toujours ici le produit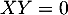
, par définition de 
.
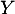De plus, on a facilement que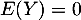
et ainsi le deuxième terme est aussi nul.
Finalement, la covariance de ces variables est nulle.
Attention, cela ne signifie pas que ces variables aléatoires sont indépendantes. Au contraire même ces variables sont clairement dépendantes: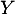
est définie à partir de 
.
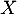On le démontre, par exemple avec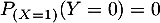
qui est bien différent
de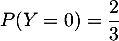 
.
On a toujours ici le produit
, par définition de .
De plus, on a facilement que
et ainsi le deuxième terme est aussi nul.
Finalement, la covariance de ces variables est nulle.
Attention, cela ne signifie pas que ces variables aléatoires sont indépendantes. Au contraire même ces variables sont clairement dépendantes:
est définie à partir de .
On le démontre, par exemple avec
qui est bien différent
de .