Colles de mathématiques
Exponentielle et logarithme
Oral HEC - filière B/L, 2022
Exercice de maths: Variables aléatoires continues - Annales HEC - B/L
Sujet
oral HEC, BL - 2022
- Question de cours : Fonction de répartition et densité d'une variable aléatoire suivant la loi exponentielle de paramètre
 .
.
-
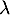 désigne un réel strictement positif. On considère la fonction
désigne un réel strictement positif. On considère la fonction 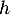 définie sur
définie sur 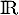 par:
par:
![\[h(x)=\la\begin{array}{cll}\lambda^2xe^{-\lambda x}&\text{si}&x\geqslant0 \\0 &\text{si} &x<0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1/5.png)
- Montrer que
 peut être considérée comme la densité de probabilité d'une variable aléatoire
peut être considérée comme la densité de probabilité d'une variable aléatoire 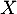 .
.
- Montrer que
 admet une espérance et la calculer.
admet une espérance et la calculer.
- Montrer que
- Dans cette question, on considère une variable aléatoire
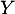 de densité
de densité 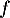 , nulle sur
, nulle sur ![$]-\infty; 0[$](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1/11.png) , continue sur
, continue sur 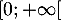 et strictement positive sur
et strictement positive sur  . On note alors
. On note alors 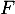 la fonction de répartition de
la fonction de répartition de  .
.
- Justifier que pour tout réel
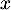 , on a
, on a 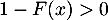 .
.
On définit alors la fonction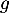 par:
par:
![\[g(x) = \la\begin{array}{cll}-f(x)\ln(1-F(x))&\text{si}&x\geqslant0\\0&\text{si}&x<0\enar\right.\]](/Generateur-Devoirs/Colles/VAC/HEC-BL-2022-3.1/19.png)
- Montrer que
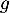 peut être considérée comme la densité d'une variable aléatoire
peut être considérée comme la densité d'une variable aléatoire  .
.
- Justifier que pour tout réel