Colles de mathématiques
Logarithme d'une loi uniforme
Sujet
Soit U une variable aléatoire de loi uniforme sur [0; 1].
Démontrer que la variable aléatoire X = − ln U suit une loi exponentielle dont on précisera le paramètre.
Démontrer que la variable aléatoire X = − ln U suit une loi exponentielle dont on précisera le paramètre.
Corrigé de l'exercice de maths: Variables aléatoires continues
Correction
On calcule la fonction de répartition de 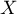 .
On a
.
On a 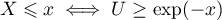 ,
puisque la fonction
,
puisque la fonction
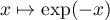 est décroissante. On a donc
est décroissante. On a donc
![\[P(X\leqslant x)=P(U\geq \exp(-x))\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-ln_c/4.png)
Si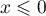 , alors
, alors 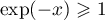 et donc
et donc 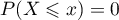 .
.
Si , alors
, alors
![$\exp(-x)\in[0,1]$](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-ln_c/9.png) et donc, puisque
et donc, puisque  suit une loi uniforme à valeurs dans
suit une loi uniforme à valeurs dans
![$[0,1]$](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-ln_c/11.png) ,
,
![\[P(X\leqslant x)=1-\exp(-x)\]](/Generateur-Devoirs/Colles/VAC/Loi-uniforme-ln_c/12.png)
et on reconnait la fonction de répartition d'une loi exponentielle de paramètre 1 (ou en dérivant pour retrouver la densité).
Si
Si
et on reconnait la fonction de répartition d'une loi exponentielle de paramètre 1 (ou en dérivant pour retrouver la densité).