Colles de mathématiques
Racine carrée d'une loi de Pareto
Retour
Exercice de maths: Variables aléatoires continues
Sujet
Soit 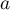 un réel et
un réel et
![\[f:\R\to\R, \, x\mapsto\la\begin{array}{cl}
0 &\text{si } x\leqslant1 \\
\dfrac{a}{x^3} &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/sqrt-pareto/2.png)
![\[f:\R\to\R, \, x\mapsto\la\begin{array}{cl}
0 &\text{si } x\leqslant1 \\
\dfrac{a}{x^3} &\text{sinon}\enar\right.\]](/Generateur-Devoirs/Colles/VAC/sqrt-pareto/2.png)
- Déterminer
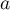 pour que
pour que  soit une densité probabilité.
soit une densité probabilité.
- Soit
 une variable aléatoire admettant
une variable aléatoire admettant 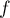 pour densité.
Déterminer la fonction de répartition de
pour densité.
Déterminer la fonction de répartition de 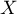 .
.
- Étudier si
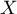 admet une espérance et une variance.
Si oui, les calculer.
admet une espérance et une variance.
Si oui, les calculer.
- Soit
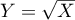 . Déterminer une densité de
. Déterminer une densité de 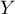 .
.
- Étudier si
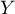 admet une espérance et une variance.
Si oui, les calculer.
admet une espérance et une variance.
Si oui, les calculer.