Colles de mathématiques
Matrice d'une application linéaire dans des bases pas canoniques
Exercice de maths: Applications linéaires - Matrices - Espaces vectoriels
Sujet
Soit 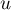 l'application linéaire de
l'application linéaire de 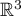 dans
dans 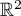 dont la matrice dans leur base
canonique respective est
dont la matrice dans leur base
canonique respective est
![\[A=\lp\begin{array}{ccc} 2&-1&1\\ 3&2&-3\enar\rp.\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2/4.png)
On appelle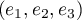 la base canonique de
la base canonique de 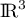 et
et 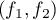 celle de
celle de 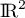 .
.
On pose
![\[e_1'=e_2+e_3,\ e_2'=e_3+e_1,\ e_3'=e_1+e_2\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2/9.png)
et
![\[f_1'=\dfrac12(f_1+f_2),\ f_2'=\dfrac12(f_1-f_2)\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases2/10.png)
On appelle
On pose
et
- Montrer que
 est une base de
est une base de 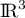 puis que
puis que 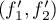 est une base de
est une base de 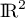 .
.
- Quelle est la matrice de
 dans ces nouvelles bases?
dans ces nouvelles bases?