🔍

Colles de mathématiques

Matrice d'une projection orthogonale - Distance à un sous-espace


Sujet


Soit E = R4 muni de son produit scalaire canonique et de la base canonique ℬ = (e1, e2, e3, e4) .
On considère G le sous-espace vectoriel défini par les équations
x1 + x2 = 0 x3 + x4 = 0
  1. Déterminer une base orthonormale de G.
  2. Déterminer la matrice dans ℬ de la projection orthogonale pG sur G.
  3. Soit x = (x1, x2, x3, x4) un élément de E. Déterminer la distance de x à G.

Corrigé de l'exercice de maths: Produit scalaire dans Rn - Espaces euclidiens - Projecteurs - Matrices

Correction


  1. On commence par trouver une base de G. Mais on a
    \[\la\begin{array}{rcl} x_1+x_2&=&0\\ x_3+x_4&=&0\\ \enar\right. \iff\la\begin{array}{rcl} x_1&=&x_1\\ x_2&=&-x_1\\ x_3&=&x_3\\ x_4&=&-x_3. \enar\right.\]

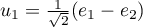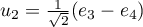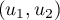    On en déduit que $(e_1-e_2,e_3-e_4)$ est une base de G. Ces deux vecteurs sont déjà orthogonaux, il suffit de les normaliser. Si on pose $u_1=\frac1{\sqrt 2}(e_1-e_2)$, $u_2=\frac1{\sqrt 2}(e_3-e_4)$, alors $(u_1,u_2)$ est une base orthonormale de $G$.
  2. On calcule $p_G(e_i)$ par
    \[p_G(e_i)=\langle e_i,u_1\rangle u_1+\langle e_i,u_2\rangle u_2\]

    On en déduit que la matrice de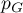 $p_G$ dans la base canonique est
    \[\frac 12\lp\begin{array}{cccc} 1&-1&0&0\\ -1&1&0&0\\ 0&0&1&-1\\ 0&0&-1&1 \enar\rp\]


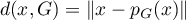  3. On sait que $d(x,G)=\|x-p_G(x)\|$.
    Avec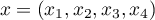 $x=(x_1,x_2,x_3,x_4)$, on a
    \[p_G(x)=\dfrac 12(x_1-x_2,-x_1+x_2,x_3-x_4,-x_3+x_4)\]

    et donc
    \[x-p_G(x)=\dfrac 12(x_1+x_2,x_1+x_2,x_3+x_4,x_3+x_4).\]

    Il vient
    \[d(x,G)^2=\dfrac 12\lp(x_1+x_2)^2+(x_3+x_4)^2\rp.\]