Colles de mathématiques
Pannes multiples sur une machine - loi exponentielle
Sujet
Le fonctionnement d'une machine est perturbé par des pannes.
On considère les variables aléatoires 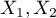 et
et 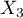 définies par:
définies par:
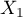 est le temps, exprimé en heures, écoulé entre la mise en route de la machine et la première panne.
est le temps, exprimé en heures, écoulé entre la mise en route de la machine et la première panne.
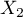 (resp.
(resp. 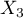 ), est le temps, en heures, écoulé entre la remise en route de la machine après la première (resp.
la deuxième) panne et la panne suivante. On suppose que les variables aléatoires
), est le temps, en heures, écoulé entre la remise en route de la machine après la première (resp.
la deuxième) panne et la panne suivante. On suppose que les variables aléatoires  et
et  sont indépendantes
et suivent la même loi exponentielle de paramètre 1/2.
sont indépendantes
et suivent la même loi exponentielle de paramètre 1/2.
- Quelle est la durée moyenne de fonctionnement entre deux pannes consécutives?
- Soit
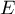 l'événement: "chacune des 3 périodes de fonctionnement de la machine dure plus de 2 heures".
Calculer
l'événement: "chacune des 3 périodes de fonctionnement de la machine dure plus de 2 heures".
Calculer 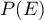 .
.
- Soit
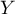 la variable aléatoire égale à la plus grande des 3 durées de fonctionnement de la machine sans interruption.
la variable aléatoire égale à la plus grande des 3 durées de fonctionnement de la machine sans interruption.
- Calculer
 pour tout
pour tout 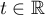 .
.
- Déterminer une densité de
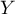 .
.
- Pour
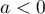 , calculer
, calculer 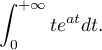
- Démontrer que la variable aléatoire
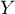 admet une espérance, dont on calculera, en heures et minutes, la valeur.
admet une espérance, dont on calculera, en heures et minutes, la valeur.
- Calculer
Corrigé de l'exercice de maths: Variables aléatoires continues
Correction
- La durée moyenne de fonctionnement entre deux pannes consécutives est l'espérance (commune) des variables aléatoires
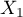 ,
, 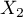 et
et 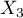 , c'est-à-dire
, c'est-à-dire 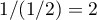 .
.
- L'événement
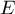 s'écrit :
s'écrit : 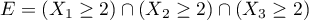 . Les variables aléatoires
. Les variables aléatoires  ,
, 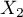 et
et 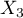 étant indépendantes,
on a
étant indépendantes,
on a 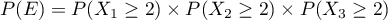 . Or,
. Or,
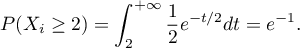
On en conclut que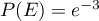 .
.
-
- On a
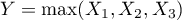 et donc
et donc  .
.
Par indépendance des 3 variables aléatoires, on en déduit que
![\[P(Y\leq t)=P(X_1\leq t)P(X_2\leq t)P(X_3\leq t)\]](/Generateur-Devoirs/Colles/VAC/panne-machine_c/15.png)
Ainsi, si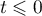 ,
, 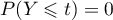 .
Si
.
Si 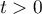 , alors
, alors
![\[P(Y\leqslant t)=\left(1-e^{-t/2}\right)^3\]](/Generateur-Devoirs/Colles/VAC/panne-machine_c/19.png)
- La quantité calculée à la question précédente est la fonction
de répartition
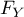 de
de 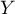 .
.
Elle est est continue sur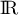 et
et  sur
sur 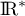 .
On en déduit que
.
On en déduit que 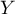 admet une densité
admet une densité  définie sur
définie sur 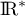 par
par 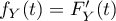 , soit
, soit
![\[f_Y(t)=\left\{
\begin{array}{ll}0&\text{ si }t<0\\
\dfrac32e^{-t/2}\left(1-e^{-t/2}\right)^2&\text{ si }t\geqslant0.
\enar\right.\]](/Generateur-Devoirs/Colles/VAC/panne-machine_c/29.png)
- À l'aide d'une intégration par parties, on trouve que
![\[\begin{array}{lcl}
\dsp\int_0^x te^{at}dt&=&\lb\dfrac{te^{at}}a\rb_0^x-\dsp\int_0^x \dfrac{e^{at}}adt\\[1.2em]
&=&\dfrac{x}a e^{ax}-\dfrac1a\lb\dfrac{e^{ax}}{a}\rb_0^x\\[1.2em]
&=&\dfrac{x}a e^{ax}-\dfrac{e^{ax}}{a^2}+\dfrac{1}{a^2}.
\enar\]](/Generateur-Devoirs/Colles/VAC/panne-machine_c/30.png)
En faisant tendre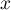 vers
vers 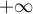 , on trouve finalement que
, on trouve finalement que
![\[\int_0^{+\infty}t e^{-at}dt=\dfrac{1}{a^2}\]](/Generateur-Devoirs/Colles/VAC/panne-machine_c/33.png)
- Pour tout
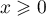 ,
,
![\[\begin{array}{r}
\dsp\int_0^x tf_Y(t)dt=\dsp\int_0^x \dfrac32te^{-t/2}(1-e^{-t/2})^2dt\\[1.2em]
=\dfrac32\dsp\int_0^x \big(te^{-t/2}-2te^{-t}+te^{-3t/2}\big)dt
\enar\]](/Generateur-Devoirs/Colles/VAC/panne-machine_c/35.png)
et, lorsque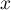 tend vers
tend vers  et d'après la question précédente, on obtient que l'intégrale
et d'après la question précédente, on obtient que l'intégrale  converge, et vaut
converge, et vaut
![\[E(Y)=\dfrac{3}2\lp\dfrac1{(-1/2)^2}-\dfrac2{(-1)^2}+\dfrac1{(-3/2)^2}\rp=\dfrac{11}{3}\]](/Generateur-Devoirs/Colles/VAC/panne-machine_c/39.png)
La durée maximale moyenne de fonctionnement entre deux pannes est 3h40min.
- On a