Colles de mathématiques
Propriété des suites arithmétiques et application
Retour
Sujet
- Montrer que une suite
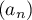 est arithmétique si et seulement si,
pour tout entier
est arithmétique si et seulement si,
pour tout entier  ,
,
![\[a_n=\dfrac{a_{n-1}+a_{n+1}}2\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique/3.png)
(Indication: on pourra s'intéresser à la suite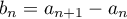 )
)
- On considère une suite
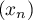 définie par
définie par 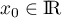 ,
,  tels que
tels que 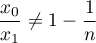 pour tout entier non nul
pour tout entier non nul 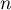 , et, pour tout entier
, et, pour tout entier 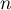 ,
,
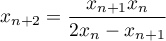 .
.
Déterminer l'expression de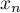 en fonction de
en fonction de 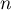 ,
,  et
et 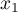 .
.
(Indication: on pourra s'intéresser à la suite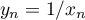 )
)
Corrigé de l'exercice de maths: Suites
Correction
- Si
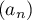 est arithmétique, alors
est arithmétique, alors 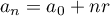 et donc
et donc
![\[\begin{array}{ll}\dfrac{a_{n-1}+a_{n+1}}2&=\dfrac{a_0+(n-1)r+a_0+(n+1)r}2\\
&=a_0+nr=a_n\enar\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique_c/3.png)
Réciproquement, supposons que pour tout entier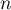 ,
,
![\[a_n=\dfrac{a_{n-1}+a_{n+1}}2\iff2a_n=a_{n-1}+a_{n+1}
\iff a_{n+1}-a_n=a_n-a_{n-1}\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique_c/5.png)
soit, en posant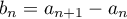 ,
,
![\[b_n=b_{n-1}\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique_c/7.png)
ce qui montre que cette suite est constante et donc que la suite est arithmétique.
est arithmétique.
- On considère une suite
 définie par
définie par 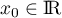 ,
,  tels que
tels que 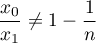 et, pour tout entier
et, pour tout entier 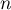 ,
,
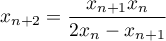 .
.
Déterminer l'expression de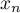 en fonction de
en fonction de 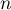 ,
, 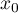 et
et 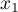 .
.
Soit , alors
, alors
![\[\begin{array}{ll}&x_{n+2}=\dfrac{x_{n+1}x_n}{2x_n-x_{n+1}}\\[1em]
&\iff y_{n+2}=2y_{n+1}-y_n\\[.8em]
&\iff y_{n+1}=\dfrac{y_{n+2}+y_n}2\enar\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique_c/20.png)
ce qui montre que la suite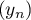 , à l'aide la question précédente, est arithmétique, et donc que
, à l'aide la question précédente, est arithmétique, et donc que
![\[y_n=\dfrac1{x_n}=y_0+nr
\iff x_n=\dfrac1{y_0+nr}\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique_c/22.png)
avec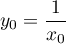 et la raison
et la raison
![\[r=y_{n+1}-y_n=y_1-y_0=\dfrac1{x_1}-\dfrac1{x_0}\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique_c/24.png)
Les suites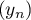 et
et  sont bien définies si
sont bien définies si
![\[\begin{array}{ll}y_0+nr\not=0
&\iff\dfrac1{x_0}+n\lp\dfrac1{x_1}-\dfrac1{x_0}\rp\not=0\\[1.em]
&\iff1+n\lp\dfrac{x_0}{x_1}-1\rp\not=0\\[1.em]
&\iff\dfrac{x_0}{x_1}\not=1-\dfrac1n\enar\]](/Generateur-Devoirs/Colles/Suites/exPropriete-suite-arithmetique_c/27.png)