🔍

Colles de mathématiques

Racines d'un trinome aléatoire


Sujet


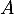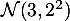On considère l'équation $x^2-Ax+1=0$ où le coefficient $A$ est une variable aléatoire qui suit la loi normale $\mathcal{N}(3,2^2)$.
Calculer la probabilité que cette équation admette deux racines réelles ?
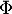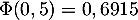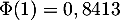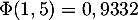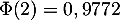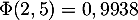On donne les valeurs de la fonction de répartition $\Phi$ de la loi normale centrée réduite: $\Phi(0,5)=0,6915$, $\Phi(1)=0,8413$, $\Phi(1,5)=0,9332$, $\Phi(2)=0,9772$, et $\Phi(2,5)=0,9938$.

Corrigé de l'exercice de maths: Variables aléatoires continues

Correction


Le trinôme admet deux racines réelles lorsque son discriminant est positif, soit
\[\Delta=A^2-4\geqslant0\]

avec la probabilité
\[\begin{array}{ll}P(\Delta\geqslant0)\\ &=P(A^2\geqslant4)\\ &=1-P(A^2\leqslant4)\\ &=1-P(-2\leqslant A\leqslant2)\enar\]

On se ramène alors à une loi normale centrée réduite en posant
\[Y=\dfrac{A-\mu}\sigma=\dfrac{A-3}2\]

et on a alors
\[\begin{array}{ll}P(\Delta\geqslant0)=1-P(-2,5\leqslant X\leqslant-0,5)\\ &=1-\lp\Phi(-0,5)-\Phi(-2,5)\rp\\ &=1-(1-\Phi(0,5))+(1-\Phi(2,5))\\ &=1-\Phi(2,5)+\Phi(0,5)\enar\]

et donc, avec les données numériques fournies,
\[\begin{array}{ll}P(\Delta\geqslant0)&=1-0,9938+0,6915\\&=0,6977\enar\]