🔍

Colles de mathématiques

Série exponentielle et termes pairs d'une loi de Poisson

Oral HEC - filière B/L, 2022


Sujet


oral HEC, BL - 2022
  1. Calculer la valeur de chacunes des sommes:
    \[S=\sum_{p=0}^{+\infty}\dfrac{\lambda^{2p}}{(2p)!}\]

    et
    \[I=\sum_{p=0}^{+\infty}\dfrac{\lambda^{2p+1}}{(2p+1)!}\]


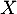  2. Soit $X$ une variable aléatoire définie sur l'espace probabilisé $(\Omega, A, P)$ suivant la loi de Poisson de paramètre $\lambda>0$. Pour tout 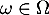$\omega\in\Omega$, on pose
    \[Y(\omega)=\la\begin{array}{lll} 0 &\text{si}&X(\omega) \text{ est nul ou impair}\\ X(\omega)/2&\text{si}& X(\omega) \text{ est pair} \enar\right.\]

    Déterminer la loi de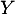 $Y$. La variable aléatoire 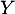$Y$ admet-elle une espérance ? Si oui, la calculer.

Corrigé de l'exercice de maths: Variables aléatoires continues - Annales HEC - B/L

Correction


oral HEC, BL - 2022 - Exercice sans préparation.
  1. La série exponentielle est
    \[e^\lambda=\sum_{p=0}^{+\infty}\dfrac{\lambda^p}{p!}\]

    On remarque alors qu'ici, on a
    \[S+I=e^\lambda\]

    tandis que
    \[S-I=\sum_{p=0}^{+\infty}\dfrac{(-\lambda)^p}{p!}=e^{-\lambda}\]

    et on trouve alors, par somme et différence,
    \[S=\dfrac{e^{\lambda}+e^{\lambda}}2=ch(\lambda)\]

    et
    \[I=\dfrac{e^{\lambda}-e^{\lambda}}2=sh(\lambda)\]


  2. On rappelle que pour une loi de Poisson, on a $P(X=k)=e^{-\lambda}\dfrac{\lambda^k}{k!}$.
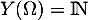    Ici, on a $Y(\Omega)=\N$ avec
    \[\begin{array}{ll}P(Y=0)&=P(X=0)+\dsp\sum_{p=1}^{+\infty}P(X=2p+1)\\ &=e^{-\lambda}+\dsp\sum_{p=1}^{+\infty}e^{-\lambda}\dfrac{\lambda^{2p+1}}{(2p+1)!} \enar\]

    soit, grâce à la première question,
    \[\begin{array}{ll}P(Y=0)&=e^{-\lambda}+e^{-\lambda}\dfrac{e^{\lambda}-e^{\lambda}}2\\ &=e^{-\lambda}\dfrac{2+e^{\lambda}-e^{-\lambda}}2\enar\]

    et, pour tout entier non nul $k$,
    \[\begin{array}{ll}P(Y=k)&=P(X=2k)\\ &=e^{-\lambda}\dfrac{\lambda^{2k}}{(2k)!}\enar\]




    L'espérance de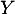 $Y$, si elle existe, est donnée par
    \[\begin{array}{ll}E(Y)&=\dsp\sum_{k=0}^{+\infty} kP(X=k)\\ &=\dsp\sum_{k=0}^{+\infty}ke^{-\lambda}\dfrac{\lambda^{2k}}{(2k)!}\\ &=e^{-\lambda}\dsp\sum_{k=0}^{+\infty}k\dfrac{\lambda^{2k}}{(2k)!}\enar\]

    On se ramène à la série exponentielle, à la série $I$ plus précisément, pour montrer que la série converge et calculer sa valeur
    \[\begin{array}{ll}E(Y)&=\dfrac{e^{-\lambda}}2\dsp\sum_{k=0}^{+\infty}2k\dfrac{\lambda^{2k}}{(2k)!}\\ &=\dfrac{\lambda e^{-\lambda}}2\dsp\sum_{k=0}^{+\infty}\dfrac{\lambda^{2k-1}}{(2k-1)!}\\ &=\dfrac{\lambda e^{-\lambda}}2 I\\ &=\dfrac{\lambda e^{-\lambda}}2 \dfrac{e^{\lambda}-e^{-\lambda}}2\\ &=\dfrac\lambda4(1-e^{-2\lambda}) \enar\]