Colles de mathématiques
Suite homographique avec un paramètre
Sujet
Soit  .
On définit
.
On définit 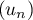 par
par  , puis,
pour tout entier
, puis,
pour tout entier 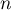 ,
,
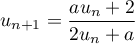
- Montrer que
 est défini pour tout
est défini pour tout 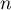 et que
et que  .
.
- On pose, pour tout
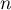 ,
,
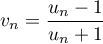 .
.
Trouver une relation entre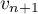 et
et 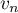 ,
et en déduire une expression de
,
et en déduire une expression de 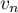 en fonction
de
en fonction
de 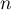 ,
, 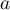 et
et 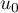 .
.
- Exprimer
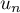 en fonction de
en fonction de 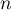 .
.
Corrigé de l'exercice de maths: Suites
Correction
- Par une récurrence immédiate, comme
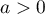 ,
si
,
si 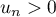 on a alors
on a alors 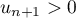 .
.
Or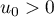 , et donc pour tout entier
, et donc pour tout entier 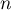 ,
, 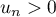 .
.
En particulier, on a aussi ce qui montre
que
ce qui montre
que 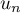 est bien toujours défini.
est bien toujours défini.
- Pour tout entier
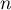 , on a
, on a
![\[\begin{array}{ll}
v_{n+1}&=\dfrac{u_{n+1}-1}{u_{n+1}+1}
=\dfrac{\dfrac{au_n+2}{2u_n+a}-1}{\dfrac{au_n+2}{2u_n+a}+1}\\[2.5em]
&=\dfrac{(a-2)u_n+2-a}{(a+2)u_n+2+a}\\[1.6em]
&=\dfrac{a-2}{a+2}\dfrac{u_n-1}{u_n+1}\\[1.6em]
&=\dfrac{a-2}{a+2}v_n
\enar\]](/Generateur-Devoirs/Colles/Suites/ex13_c/10.png)
ce qui montre que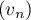 est géométrique de raison
est géométrique de raison
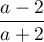 .
.
- On a alors
![\[\begin{array}{ll}
v_n=\dfrac{u_n-1}{u_n+1}
&\iff
v_n\left( u_n+1\rp=u_n-1 \\[.8em]
&\iff
u_n\left( v_n-1\rp=-1-v_n\\[.8em]
&\iff
u_n=\dfrac{-1-v_n}{v_n-1}=\dfrac{1+v_n}{1-v_n}
\enar\]](/Generateur-Devoirs/Colles/Suites/ex13_c/13.png)
soit, avec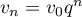 , avec
, avec 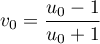 et
et 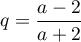 ,
,
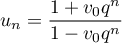 .
.