Colles de mathématiques
Bases de sous-espaces vectoriels
Sujet
Soit 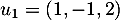 ,
, 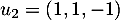 et
et 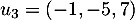 .
.
On pose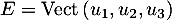 et
et
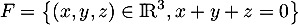 .
.
On pose
- Donner une base de
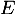 .
.
- Montrer que
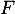 est un sous-espace vectoriel de
est un sous-espace vectoriel de  ,
et en donner une base.
,
et en donner une base.
- Donner une base de
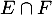 .
.
Corrigé de l'exercice de maths: Espaces vectoriels
Correction
- On a
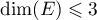 .
Il reste à voir si les trois vecteurs forment une famille libre ou non.
.
Il reste à voir si les trois vecteurs forment une famille libre ou non.
![\[\begin{array}{rl}\alpha u_1+\beta u_2+\gamma u_3=0
&\iff\la\begin{array}{rcrcrcl}
\alpha&+&\beta&-&\gamma&=&0 \\
-\alpha&+&\beta&-&5\gamma&=&0\\
2\alpha&-&\beta&+&7\gamma&=&0\enar\right.\\[2em]
\begin{array}{r}\\L_1+L_2\to L_2\\2L_1+L_3\to L_3\end{array}
&\iff\la\begin{array}{rcrcrcl}
\alpha&+&\beta&-&\gamma&=&0 \\
&&2\beta&-&6\gamma&=&0\\
&-&3\beta&+&9\gamma&=&0\enar\right.\\[2em]
&\iff\la\begin{array}{rcrcrcl}
\alpha&+&\beta&-&\gamma&=&0 \\
&&\beta&&&=&3\gamma\\
&&\beta&&&=&3\gamma\enar\right.
\enar\]](/Generateur-Devoirs/Colles/ev/ex1.5_c/2.png)
La famille n'est donc pas libre, et en choisissant par exemple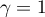 et donc
et donc 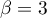 et
et  , on obtient la relation
, on obtient la relation
![\[-2u_1+3u_2+u_3=0\iff u_3=2u_1-3u_2\]](/Generateur-Devoirs/Colles/ev/ex1.5_c/6.png)
On a donc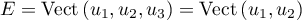 ,
et comme
,
et comme 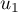 et
et 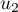 ne sont pas liés (ils ne sont pas proportionnels),
on en déduit qu'ils forment une base de
ne sont pas liés (ils ne sont pas proportionnels),
on en déduit qu'ils forment une base de 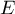 .
.
-
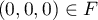 , et
si
, et
si 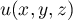 et
et 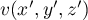 , donc
, donc 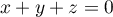 et
et 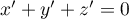 ,
alors
,
alors 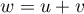 est tel que
est tel que
 avec
avec
![\[(x+x')+(y+y')+(z+z')=\left( x+y+z\rp+\left( x'+y'+z'\rp=0\]](/Generateur-Devoirs/Colles/ev/ex1.5_c/18.png)
et donc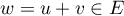 .
.
De même, si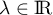 ,
alors
,
alors  est tel que
est tel que
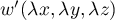 avec
avec
![\[(\lambda x)+(\lambda y)+(\Lambda z)
=\lambda (x+y+z)=0\]](/Generateur-Devoirs/Colles/ev/ex1.5_c/23.png)
et donc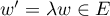 .
.
Ainsi,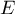 est un sous-espace vectoriel de
est un sous-espace vectoriel de  .
.
Pour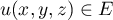 , on a
, on a  et donc
et donc 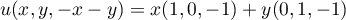 .
.
Ainsi,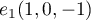 et
et  forment une famille génératrice de
forment une famille génératrice de 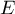 .
Comme ces vecteurs ne sont pas liés, ils forment de plus une base de
.
Comme ces vecteurs ne sont pas liés, ils forment de plus une base de  .
.
- Soit
 , alors
, alors
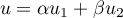 et
et 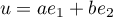 et donc
et donc
![\[\begin{array}{rl}\alpha u_1+\beta u_2=u=a e_1+be_2
&\iff
\la\begin{array}{rcrlcl}
\alpha&+&\beta&=&a\\
-\alpha&+&\beta&=&b\\
2\alpha&-&\beta&=&-a-b
\enar\right.\\[2em]
&\iff
\la\begin{array}{rcrcrcrlcl}
\alpha&+&\beta&-&a&&&=&0\\
-\alpha&+&\beta&& &-&b&=&0\\
2\alpha&-&\beta&+&a&+&b&=&0
\enar\right.\\[2em]
\begin{array}{r}\\L_1+L_2\to L_2\\2L_1-L_3\to L_3\end{array}
&\iff
\la\begin{array}{rcrcrcrlcl}
\alpha&+&\beta&-&a&&&=&0\\
&+&2\beta&-&a&-&b&=&0\\
&&3\beta&-&3a&-&b&=&0
\enar\right.\\[2em]
\begin{array}{r}\\\\3L_2-2L_3\to L_3\end{array}
&\iff
\la\begin{array}{rcrcrcrlcl}
\alpha&+&\beta&-&a&&&=&0\\
&+&2\beta&-&a&-&b&=&0\\
&&&&3a&-&b&=&0
\enar\right.\\[2em]
\enar\]](/Generateur-Devoirs/Colles/ev/ex1.5_c/37.png)
On trouve donc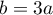 , puis
, puis 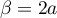 et
et  , soit
, soit
![\[u=\alpha u_1+\beta u_2=a(1,3,-4)\]](/Generateur-Devoirs/Colles/ev/ex1.5_c/41.png)
ou ce qu'on (doit) retrouve(r) avec la deuxième relation:
![\[u=ae_1+be_2=a(1,3,-4)\]](/Generateur-Devoirs/Colles/ev/ex1.5_c/42.png)
Ainsi, en posant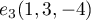 on a
on a
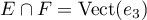 , et
, et 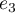 est une base de ce sous-espace de dimension 1.
est une base de ce sous-espace de dimension 1.