🔍

Colles de mathématiques

Egalité de sous-espaces vectoriels et supplémentaire


Retour


Exercice de maths: Espaces vectoriels

Sujet


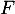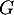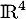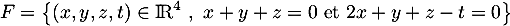
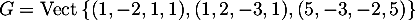Soit $F$ et $G$ les sous-espaces vectoriels de $\R^4$ suivants: $F=\left\{ (x,y,z,t)\in \R^4 \ , \ x+y+z=0 \text{ et } 2x+y+z-t=0 \right\}$ $G=\text{Vect}\left\{ (1,-2,1,1),(1,2,-3,1),(5,-3,-2,5)\right\}$.
  1. Montrer que 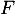$F$ est un espace vectoriel et donner sa dimension de $F$.
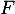  2. Montrer que 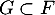$G\subset F$ et conclure que $G=F$.
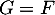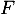  3. Déterminer un supplémentaire de $F$.

Correction