🔍

Colles de mathématiques

Caractérisation d'une similitude


Sujet


Soit E = Rn muni du produit scalaire canonique, f∈ℒ(E) et λ>0. On dit que f est une similitude de rapport λ si pour tout x∈E, ||f(x)|| = λ||x||.
  1. Soit u, v∈E tels que u+v⊥u−v. Démontrer que ||u|| = ||v||.
  2. Démontrer que f est une similitude de rapport λ si et seulement si, pour tous x, y∈E, ⟨f(x), f(y)⟩ = λ2⟨x, y⟩.
  3. On souhaite prouver que f est une similitude si et seulement f est non-nulle et conserve l'orthogonalité: pour tout couple (x, y)∈E2, si x⊥y, alors f(x)⊥f(y).
    1. Prouver le sens direct.
    2. Soit (e1, …, en) une base orthonormale de E. Démontrer que, pour tout couple (i, j), on a ||f(ei)|| = ||f(ej)||.
    3. Démontrer le sens réciproque.

Corrigé de l'exercice de maths: Produit scalaire dans Rn - Espaces euclidiens

Correction


  1. On a, en utilisant la bilinéarité et la symétrie du produit scalaire,
    \[\begin{array}{ll}\langle u+v,u-v\rangle&=\|u\|^2- \langle u,v\rangle +\langle v,u\rangle -\|v\|^2\\ &=\|u\|^2-\|v\|^2\enar\]

    et ainsi,
    \[\langle u+v,u-v\rangle=0 \iff \|u\|^2=\|v\|^2\]

  2. Bien sûr, le sens réciproque est trivial puisqu'il suffit de choisir $x=y$.
    Réciproquement, supposons que pour tout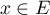 $x\in E$, on a 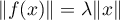$\|f(x)\|=\lambda\|x\|$. Alors, d'une part
    \[\begin{array}{ll} \|f(x+y)\|^2&=\|\lambda(x+y)\|^2\\[.4em] &=\lambda^2\|x+y\|^2\\[.4em] &=\lambda^2\langle x+y,x+y\rangle\\[.4em] &=\lambda^2\Bigl( \|x\|^2+2\langle x,y\rangle +\|y\|^2\Bigr) \enar\]

    et d'autre part
    \[\begin{array}{ll}\|f(x+y)\|^2&=\langle f(x+y),f(x+y)\rangle\\[.4em] &=\|f(x)\|^2+2\langle f(x),f(y)\rangle+\|f(y)\|^2\\[.5em] &=\lambda^2\|x\|^2+2\langle f(x),f(y)\rangle+\lambda^2\|y\|^2\end{array} \]

    En égalant ces deux dernières relations, on obtient donc
    \[\langle f(x),f(y)\rangle=\lambda^2 \langle x,y\rangle\]


    1. C'est une conséquence directe de la question précédente.
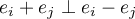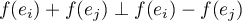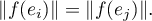
    2. On sait que $e_i+e_j\perp e_i-e_j$. Puisque f préserve l'orthogonalité, $f(e_i)+f(e_j)\perp f(e_i)-f(e_j)$. Et d'après la première question, $\|f(e_i)\|=\|f(e_j)\|.$
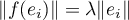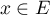    3. Soit λ>0 tel que $\|f(e_i)\|=\lambda \|e_i\|$  ( λ ne dépend pas de $i$ d'après la question précédente, et est strictement positif sinon f serait nulle). On va démontrer que f est une similitude de rapport λ. Soit $x\in E$ qui s'écrit
      \[x=\sum_{i=1}^n x_i e_i\]

      Alors
      \[f(x)=\sum_{i=1}^n x_if(e_i)\]

      La famille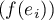 $(f(e_i))$ étant orthogonale, on a
      \[\begin{array}{lcl} \|f(x)\|^2&=&\dsp\sum_{i=1}^n |x_i|^2\|f(e_i)\|^2\\ &=&\lambda^2\dsp\sum_{i=1}^n |x_i|^2\\[1.2em] &=&\lambda^2\|x\|^2. \enar\]

      f est bien une similitude de rapport λ.