Colles de mathématiques
Concentration des lois uniformes
Sujet
Soit 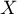 une variable aléatoire suivant une loi uniforme sur
une variable aléatoire suivant une loi uniforme sur ![$[a,b]$](/Generateur-Devoirs/Colles/VAC/Concentration-loi-uniforme/2.png) . On note
. On note  sa moyenne et
sa moyenne et 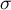 son écart-type.
son écart-type.
Calculer la probabilité![$P(X\in [m-\sigma,m+\sigma])$](/Generateur-Devoirs/Colles/VAC/Concentration-loi-uniforme/5.png) .
.
Calculer la probabilité
Corrigé de l'exercice de maths: Variables aléatoires continues
Correction
La densité de probabilité de la loi uniforme sur ![$[a;b]$](/Generateur-Devoirs/Colles/VAC/Concentration-loi-uniforme_c/1.png) est
est
![$f(x)=\dfrac{1}{b-a}\mathbf 1_{[a,b]}(x)$](/Generateur-Devoirs/Colles/VAC/Concentration-loi-uniforme_c/2.png) .
.
On sait aussi que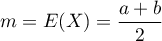 et
et 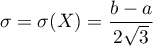 (ou le redémontrer).
(ou le redémontrer).
On remarque aussi que
![\[m+\sigma=\dfrac{a+b}2+\dfrac{b-a}{2\sqrt3}\leqslant\dfrac{a+b}2+\frac{b-a}2\leqslant b\]](/Generateur-Devoirs/Colles/VAC/Concentration-loi-uniforme_c/5.png)
et de même que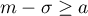 .
.
On caclule alors la probabilité:
![\[\begin{array}{lcl}
P(X\in [m-\sigma,m+\sigma])&=&\dsp\frac{1}{b-a}\int_{m-\sigma}^{m+\sigma}dt\\[.6em]
&=&\dfrac{1}{b-a}\times (m+\sigma-m+\sigma)\\[.6em]
&=&\dfrac{2\sigma}{b-a}\\[.6em]
&=&\dfrac1{\sqrt3}.
\enar\]](/Generateur-Devoirs/Colles/VAC/Concentration-loi-uniforme_c/7.png)
On remarque au passage que cette probabilité ne dépend pas de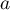 et de
et de  .
.
On sait aussi que
On remarque aussi que
et de même que
On caclule alors la probabilité:
![\[\begin{array}{lcl}
P(X\in [m-\sigma,m+\sigma])&=&\dsp\frac{1}{b-a}\int_{m-\sigma}^{m+\sigma}dt\\[.6em]
&=&\dfrac{1}{b-a}\times (m+\sigma-m+\sigma)\\[.6em]
&=&\dfrac{2\sigma}{b-a}\\[.6em]
&=&\dfrac1{\sqrt3}.
\enar\]](/Generateur-Devoirs/Colles/VAC/Concentration-loi-uniforme_c/7.png)
On remarque au passage que cette probabilité ne dépend pas de