Colles de mathématiques
Indice de nilpotence maximal dans un espace de dimension fini
Sujet
Soit f un endomorphisme non nul d'un espace de dimension fini n.
On suppose f nilpotent d'indice p, i.e.
f p−1≠0 et f p = 0.
Montrer qu'il existe x0∈E tel que la famille (x0, f (x0), f 2(x0), …, f p−1(x0)) est libre.
En déduire que f n(x0) = 0 .
Montrer qu'il existe x0∈E tel que la famille (x0, f (x0), f 2(x0), …, f p−1(x0)) est libre.
En déduire que f n(x0) = 0 .
Corrigé de l'exercice de maths: Espaces vectoriels
Correction
Par définition, 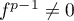 ce qui signifie justement
qu'il existe
ce qui signifie justement
qu'il existe 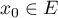 tel que
tel que 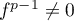 .
.
On considère alors une combinaison linéaire nulle: soit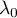 ,
, 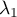 , … ,
, … , 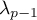 tels que
tels que
![\[\lambda_0x_0+\lambda_1f\left( x_0\rp+\lambda_2f^2\left( x_0\rp+\dots+\lambda_{p-1}f^{p-1}\left( x_0=0\]](/Generateur-Devoirs/Colles/ev/exnil_c/7.png)
Comme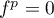 , et donc aussi
, et donc aussi 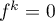 pour tout
pour tout 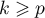 ,
en appliquant
,
en appliquant 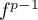 à la combinaison précédente, on obtient
à la combinaison précédente, on obtient
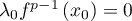 .
.
Comme on a choisit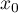 tel que
tel que 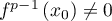 , on a donc nécessairement
, on a donc nécessairement 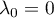 .
.
En appliquant de même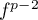 à la combinaison,
on obtient maintenant, avec
à la combinaison,
on obtient maintenant, avec 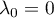 ,
,
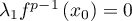 et donc, de même que précédemment,
et donc, de même que précédemment,  .
.
En réitérant, on obtient donc successivement ,
ce qui montre que la famille
,
ce qui montre que la famille
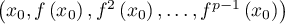 est libre.
est libre.
Il s'agit ici de montrer que l'indice de nilpotence vérifie
vérifie  .
.
Comme cette famille est libre dans un espace de dimension , elle contient nécessairement moins de
, elle contient nécessairement moins de 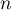 vecteurs.
Comme elle est composée de
vecteurs.
Comme elle est composée de 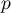 vecteurs, on a donc
vecteurs, on a donc 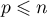 et alors, comme on l'a remarqué précédemment,
et alors, comme on l'a remarqué précédemment,
 pour tout
pour tout 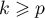 ; en particulier
; en particulier 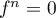 .
.
On considère alors une combinaison linéaire nulle: soit
Comme
Comme on a choisit
En appliquant de même
En réitérant, on obtient donc successivement
Il s'agit ici de montrer que l'indice de nilpotence
Comme cette famille est libre dans un espace de dimension