🔍

Colles de mathématiques

Loi exponentielle symétrique


Sujet


On considère une variable aléatoire 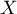$X$ dont la densité est donnée par
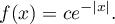
$$f(x)=ce^{-|x|}.$$

  1. Calculer $c$.
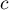  2. Démontrer que 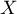$X$ admet des moments de tout ordre. Les calculer.

Corrigé de l'exercice de maths: Variables aléatoires continues

Correction


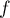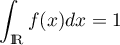  1. $f$ est continue et positive, et il faut aussi que $\dsp\int_\R f(x)dx=1$.
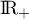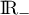    On calcule l'intégrale en séparant par la relation de Chasles $\R_+$ et $\R_-$ et on trouve $c=1/2$.
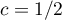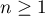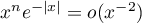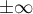  2. On a, pour tout $n\geq 1$, $x^ne^{-|x|}=o(x^{-2})$ en $\pm \infty$, ce qui prouve la convergence de l'intégrale.
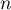    La fonction $x\mapsto x^n e^{-|x|}$ est impaire si $n$ est impair; on en déduit que les moments d'ordre impair sont nuls.
    On peut calculer les moments d'ordre pair par récurrence. Pour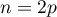 $n=2p$, posons 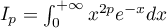$I_p=\int_0^{+\infty}x^{2p}e^{-x}dx$, de sorte que $E(X^{2p})=I_p$. Alors, en intégrant par parties (deux fois), on trouve
    \[\begin{array}{lcl} I_p&=&\dsp\int_0^{+\infty}2px^{2p-1}e^{-x}dx\\[1em] &=&\dsp\int_0^{+\infty}2p(2p-1)x^{2p-2}e^{-x}dx\\[1em] &=&2p(2p-1)I_{p-1}\enar\]


    On en déduit que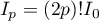 $I_p=(2p)!I_0$.
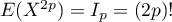    On calcule par ailleurs $I_0=1$, ce qui nous donne les moments d'ordre pair: $E(X^{2p})=I_p=(2p)!$.