Colles de mathématiques
Matrice d'une application linéaire, et changement de bases
Sujet
Soit 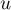 l'application de
l'application de  dans
dans 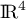 définie par
définie par
![\[
u(x,y,z)=(-x+y,x-y,-x+z,-y+z).
\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases/4.png)
- Montrer que
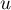 est linéaire
est linéaire
- Soient
 la base canonique de
la base canonique de  et
et 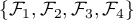 la base canonique de
la base canonique de 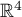 .
.
Calculer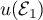 ,
, 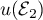 et
et 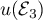 en fonction de
en fonction de 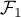 ,
, 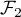 ,
, 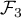 et
et  .
.
- Écrire la matrice de
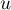 dans les bases canoniques.
dans les bases canoniques.
- Montrer que
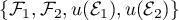 est une base de
est une base de 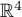 .
.
- Écrire la matrice de
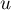 dans les bases
dans les bases
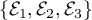 et
et 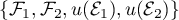 .
.
Corrigé de l'exercice de maths: Applications linéaires - Matrices - Espaces vectoriels
Correction
- Soit
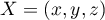 ,
, 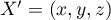 et
et 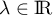 , alors
, alors
![\[\begin{array}{lcl}
u(X+X')&=&u(x+x',y+y',z+z')\\
&=&(-x-x'+y+y',x+x'-y-y',-x-x'+z+z',-y-y'+z+z')\\
&=&\big((-x+y)+(-x'+y'),(x-y)+(x'-y'),(-x+z)+(-x'+z'),\\
&&\quad\quad(-y+z)+(-y'+z')\big)\\
&=&(-x+y,x-y,-x+z,-y+z)+(-x'+y',x'-y',-x'+z',-y'+z')\\
&=&u(X)+u(X').
\enar\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/4.png)
De même, on a
![\[\begin{array}{lcl}
u(\lambda X)&=&u(\lambda x,\lambda y,\lambda z)\\
&=&u(-\lambda x+\lambda y,\lambda x-\lambda y,-\lambda x+\lambda z,-\lambda y+\lambda z)\\
&=&\lambda (-x+y,x-y,-x+z,-y+z)\\
&=&\lambda u(X).
\enar\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/5.png)
Ainsi, est linéaire.
est linéaire.
- On a
![\[\begin{array}{lcl}
u(\mathcal E_1)&=&u(1,0,0)=(-1,1,-1,0)=-\mathcal F_1+\mathcal F_2-\mathcal F_3\\
u(\mathcal E_2)&=&u(0,1,0)=(1,-1,0,-1)=\mathcal F_1-\mathcal F_2-\mathcal F_4\\
u(\mathcal E_3)&=&u(0,0,1)=(0,0,1,1)=\mathcal F_3+\mathcal F_4.
\enar\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/7.png)
- La matrice est:
![\[\lp\begin{array}{ccc}
-1&1&0\\
1&-1&0\\
-1&0&1\\
0&-1&1\\
\enar\rp\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/8.png)
- Puisque
 est de dimension 4 et que la famille a quatre éléments,
il suffit de montrer qu'elle est libre.
est de dimension 4 et que la famille a quatre éléments,
il suffit de montrer qu'elle est libre.
C'est bien le cas ici, car si ,
alors
,
alors
![\[\la\begin{array}{rcl}
a-c+d&=&0\\
b+c-d&=&0\\
-c&=&0\\
-d&=&0
\enar\right.
\iff a=b=c=d=0.\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/11.png)
- Il s'agit d'exprimer chaque
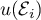 en fonction des vecteurs de la nouvelle base.
en fonction des vecteurs de la nouvelle base.
Pour deux des vecteurs, on a directement que et
et 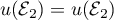 .
.
Pour le troisième, il faut trouver de sorte que
de sorte que
![\[a\mathcal F_1+b\mathcal F_2+cu(\mathcal E_1)+du(\mathcal E_2)=(0,0,1,1)\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/16.png)
Ceci revient à résoudre le système
![\[\la\begin{array}{rcl}
a-c+d&=&0\\
b+c-d&=&0\\
c&=&-1\\
d&=&-1
\enar\right.
\iff\la\begin{array}{rcl}
a&=&0\\
b&=&0\\
c&=&-1\\
d&=&-1
\enar\right.\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/17.png)
Ainsi, on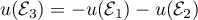 et la matrice de
et la matrice de 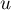 dans les bases
dans les bases
 et
et 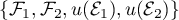 est donc
est donc
![\[\lp\begin{array}{ccc}
0&0&0\\
0&0&0\\
1&0&-1\\
0&1&-1
\enar\rp\]](/Generateur-Devoirs/Colles/matrices/exALchgtBases_c/22.png)