Colles de mathématiques
Matrice d'une projection orthogonale dans l'espace
Sujet
Soit E = R3 muni de sa structure euclidienne canonique.
Soit p∈ℒ(E) dont la matrice dans la base canonique est
Déterminer la distance de (1, 1, 1) à ce plan.
A = 16
5
−2
1
−2
2
2
1
2
5
Montrer que p est une projection orthogonale sur un plan
dont on précisera l'équation.Déterminer la distance de (1, 1, 1) à ce plan.
Corrigé de l'exercice de maths: Produit scalaire dans Rn - Espaces euclidiens - Projecteurs - Matrices
Correction
On commence par remarquer que  .
Ainsi,
.
Ainsi, 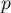 est bien une projection.
On va déterminer
est bien une projection.
On va déterminer 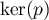 et
et 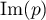 .
Il suffira ensuite de démontrer que ces deux sous-espaces sont orthogonaux pour pouvoir conclure.
On remarque d'abord que
.
Il suffira ensuite de démontrer que ces deux sous-espaces sont orthogonaux pour pouvoir conclure.
On remarque d'abord que 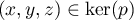 si et seulement si
si et seulement si
![\[\begin{array}{lcl}
\la\begin{array}{rcl}
5x-2y+z&=&0\\
-2x+2y+2z&=&0\\
x+2y+5z&=&0\\
\enar\right. &\iff&
\la\begin{array}{rcl}
x+2y+5z&=&0\\
6y+12z&=&0\\
-12y-24z&=&0\\
\enar\right.\\
&\iff&
\la\begin{array}{rcl}
x&=&-z\\
y&=&-2z\\
z&=&z
\enar\right.\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex1_c/6.png)
Ainsi,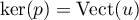 , où
, où 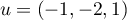 .
On en déduit (on sait déjà que
.
On en déduit (on sait déjà que  est une projection) que
est une projection) que  est de dimension 2.
Puis, puisque
est de dimension 2.
Puis, puisque 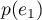 et
et 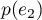 sont indépendants, en posant
sont indépendants, en posant 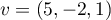 et
et 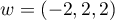 ,
on en déduit que
,
on en déduit que 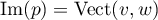 .
.
Pour démontrer que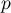 est une projection orthogonale, il reste à prouver que
est une projection orthogonale, il reste à prouver que 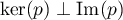 .
Mais
.
Mais  et
et 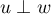 , donc on a bien
, donc on a bien 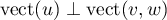 .
.
Puisque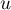 est un vecteur normal au plan
est un vecteur normal au plan 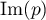 , une équation de ce plan est
, une équation de ce plan est
![\[-x-2y+z=0.\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex1_c/23.png)
Enfin, la distance de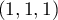 au plan
au plan  par:
par:
![\[d=\frac{|\langle u,(1,1,1)\rangle|}{\|u\|}=\frac{|-1-2+1|}{\sqrt 6}=\frac {2}{\sqrt 6}\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex1_c/26.png)
![\[\begin{array}{lcl}
\la\begin{array}{rcl}
5x-2y+z&=&0\\
-2x+2y+2z&=&0\\
x+2y+5z&=&0\\
\enar\right. &\iff&
\la\begin{array}{rcl}
x+2y+5z&=&0\\
6y+12z&=&0\\
-12y-24z&=&0\\
\enar\right.\\
&\iff&
\la\begin{array}{rcl}
x&=&-z\\
y&=&-2z\\
z&=&z
\enar\right.\enar\]](/Generateur-Devoirs/Colles/EspaceEuclidien/ex1_c/6.png)
Ainsi,
Pour démontrer que
Puisque
Enfin, la distance de