Colles de mathématiques
Min et max de deux lois exponentielles
Sujet
Soit 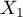 et
et 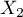 deux variables aléatoires indépendantes suivant
une loi exponentielle
de paramètres respectifs
deux variables aléatoires indépendantes suivant
une loi exponentielle
de paramètres respectifs 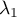 et
et  .
On pose
.
On pose 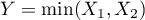 .
.
- Pour tout réel
 , calculer
, calculer 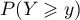 .
En déduire que
.
En déduire que 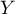 suit une loi exponentielle
de paramètre
suit une loi exponentielle
de paramètre  .
.
- Deux guichets sont ouverts à une banque. Le temps de service au premier guichet (resp. au deuxième) suit une loi exponentielle de moyenne 20 min (resp. 30 min). Deux clients rentrent simultanément, l'un choisit le guichet 1 et l'autre le guichet 2. En moyenne, après combien de temps sort le premier?
- En moyenne, après combien de temps sort le dernier.
Corrigé de l'exercice de maths: Variables aléatoires continues
Correction
- On va commencer par calculer
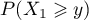 .
Si
.
Si 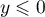 , alors
, alors 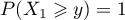 (car
(car  est à valeurs dans
est à valeurs dans 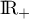 ).
).
Sinon, pour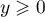 , on a
, on a
![\[P(X_1\geqslant y)
=\int_y^{+\infty}\dfrac1{\lambda_1}e^{-\lambda_1 y}dy=e^{-\lambda_1 y}\]](/Generateur-Devoirs/Colles/VAC/LoiExponentielle-min-max_c/7.png)
et de même,
![\[P(X_2\geqslant y)=e^{-\lambda_2 y}\]](/Generateur-Devoirs/Colles/VAC/LoiExponentielle-min-max_c/8.png)
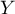 est à valeurs positives,
donc
est à valeurs positives,
donc 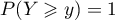 si
si  .
Si
.
Si 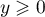 , alors
, alors
![\[P(Y\geqslant y)=P\Bigl(\left( X_1\geqslant y\rp\cap\left( X_2\geqslant y\rp\Bigr)
=P(X_1\geqslant y)P(X_2\geqslant y)
=e^{-(\lambda_1+\lambda_2)y}\]](/Generateur-Devoirs/Colles/VAC/LoiExponentielle-min-max_c/13.png)
grâce à l'indépendance de et
et 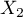 ,
et on reconnait la fonction de répartition d'une loi
exponentielle de paramètre
,
et on reconnait la fonction de répartition d'une loi
exponentielle de paramètre 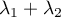 .
.
- On cherche
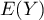 , avec
, avec  et
et 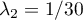 .
L'espérance de
.
L'espérance de 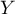 est donc
est donc
![\[E(Y)=\frac1{\lambda_1+\lambda_2}=\frac{60}5=12\]](/Generateur-Devoirs/Colles/VAC/LoiExponentielle-min-max_c/21.png)
- On cherche l'espérance de
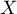 , où
, où
 est la variable aléatoire définie cette fois par
est la variable aléatoire définie cette fois par 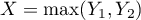 ,
On peut procéder comme à la question précédente en cherchant la fonction
de répartition de
,
On peut procéder comme à la question précédente en cherchant la fonction
de répartition de  , ou remarquer que pour tout nombre
, ou remarquer que pour tout nombre 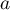 et
et  on a
on a
![\[\min(a,b)+\max(a,b)=a+b\]](/Generateur-Devoirs/Colles/VAC/LoiExponentielle-min-max_c/28.png)
soit ici
![\[X+Y=X_1+X_2\]](/Generateur-Devoirs/Colles/VAC/LoiExponentielle-min-max_c/29.png)
En prenant l'espérance, et par linéarité, on trouve
![\[E(X)=E(X_1)+E(X_2)-E(Y)=20+30-12=38\]](/Generateur-Devoirs/Colles/VAC/LoiExponentielle-min-max_c/30.png)