Colles de mathématiques
Produit de la densité et fonction de repartition d'une loi normale
Retour
Sujet
- Calculer
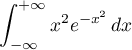 sachant que
sachant que 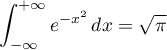
- Soit
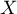 une variable aléatoire qui suit la loi normale centrée réduite.
une variable aléatoire qui suit la loi normale centrée réduite.
Soit la densité et
la densité et 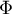 la fonction de répartition de
la fonction de répartition de  .
Pour tout réel
.
Pour tout réel  , on pose
, on pose  .
.
- Quelle relation a-t-on entre
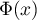 et
et  ?
?
- Quelle est la valeur de
 pour que
pour que 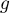 soit la densité d'une variable
aléaltoire
soit la densité d'une variable
aléaltoire 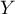 ?
?
- Calculer l'espérance et la variance de
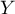 .
.
- Quelle relation a-t-on entre
Corrigé de l'exercice de maths: Variables aléatoires continues
Correction
- En intégrant par parties,
![\[\begin{array}{ll}\dsp\int_{-\infty}^{+\infty}x^2e^{-x^2}\,dx
&\dsp=\int_{-\infty}^{+\infty}x \left( xe^{-x^2}\right) dx\\[1.4em]
&\dsp=\left[ x\dfrac{e^{-x^2}}{-2}\rb_{-\infty}^{+\infty}
-\int_{-\infty}^{+\infty}\dfrac{e^{-x^2}}{-2}\,dx\\[1.4em]
&=\dfrac12\sqrt\pi\end{array}
\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/1.png)
car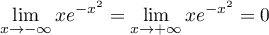 .
.
- Soit
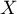 une variable aléatoire qui suit la loi normale centrée réduite.
une variable aléatoire qui suit la loi normale centrée réduite.
Soit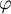 la densité et
la densité et 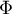 la fonction de répartition de
la fonction de répartition de 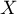 .
Pour tout réel
.
Pour tout réel 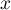 , on pose
, on pose 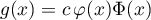 .
.
- On a
 et alors,
en posant
et alors,
en posant  et donc
et donc 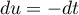 ,
,
![\[\Phi(-x)=P\left( X<-x\rp=\int_{-\infty}^{-x}\varphi(t)dt
=\int_{+\infty}^x\varphi(-u)\lp-du\rp\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/12.png)
puis, comme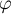 est paire,
est paire, 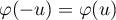 ,
,
![\[\begin{array}{ll}\Phi(-x)&\dsp=\int_x^{+\infty}\varphi(u)du\\[.8em]
&\dsp=\int_{-\infty}^{+\infty}\varphi(u)du-\int_{-\infty}^x\varphi(u)du\\[1em]
&\dsp=1-\Phi(x)
\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/15.png)
- On a clairement
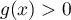 pour tout réel
pour tout réel 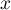 ,
et on souhaite donc aussi que
,
et on souhaite donc aussi que
![\[\int_{-\infty}^{+\infty}g(t)dt
=c\int_{-\infty}^{+\infty}\varphi(t)\Phi(t)dt
=1\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/18.png)
On pose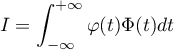 .
.
1ère méthode: avec un changement de variable.
Comme précédemment, avec le changement de variable ,
on a
,
on a
![\[I=\int_{+\infty}^{-\infty}\varphi(-u)\Phi(-u)\lp-du\rp\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/21.png)
et donc, en utilisant la parité de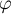 et la relation de la question
précédente
et la relation de la question
précédente
![\[\begin{array}{ll}I&=\dsp\int_{-\infty}^{+\infty}\varphi(u)\lp1-\Phi(u)\right) du\\[1.3em]
&\dsp=\int_{-\infty}^{+\infty}\varphi(u)du
-\int_{-\infty}^{+\infty}\varphi(u)\Phi(u) du\\[1.3em]
&=1-I\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/23.png)
et on trouve donc que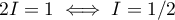 .
.
On doit donc avoir .
.
2ème méthode: avec une intégration par parties.
On a et donc
et donc
![\[\lp\Phi^2\rp'=2\Phi'\Phi=2\varphi\Phi\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/27.png)
et alors
![\[\begin{array}{ll}
I&\dsp=\int_{-\infty}^{+\infty}\varphi(t)\Phi(t)dt\\[1em]
&=\Bigl[\,\dfrac12\Phi^2(t)\,\Bigr]_{-\infty}^{+\infty}
=\dfrac12
\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/28.png)
car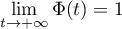 et
et
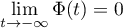 .
.
On trouve donc que nécessirement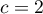 .
.
- L'espérance de
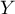 est
est
![\[E(Y)=\int_{-\infty}^{+\infty}yg(y)dx
=2\int_{-\infty}^{+\infty}y\varphi(y)\Phi(y)dy\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/33.png)
On se rappelle que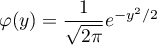 et donc
et donc 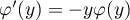 ,
et que les fonctions de densité et de répartition sont reliées
par
,
et que les fonctions de densité et de répartition sont reliées
par 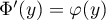 .
.
On peut donc penser à intégrer par parties avec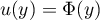 et
et 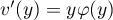 ,
donc
,
donc 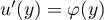 et
et 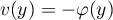 ,
et on a donc
,
et on a donc
![\[E(Y)=2\Bigl[-\Phi(y)\varphi(y)\Bigr]_{-\infty}^{+\infty}
+2\int_{-\infty}^{+\infty}\varphi^2(y)dy\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/41.png)
Comme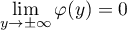 et
et 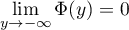 et
et 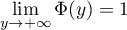 ,
on a
,
on a
![\[\Bigl[-\Phi(y)\varphi(y)\Bigr]_{-\infty}^{+\infty}=0\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/45.png)
et donc
![\[\begin{array}{ll}E(Y)
&\dsp=2\int_{-\infty}^{+\infty}\lp\dfrac1{\sqrt{2\pi}}e^{-y^2/2}\rp^2dy\\[1.5em]
&\dsp=\dfrac1\pi\int_{-\infty}^{+\infty}e^{-y^2}dy\\[1.4em]
&=\dfrac1\pi\tm\sqrt{\pi}=\dfrac1{\sqrt\pi}\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/46.png)
La variance de est
est
![\[V(Y)=E\left( Y^2\rp-\left( E(Y)\rp^2\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/48.png)
avec
![\[\begin{array}{ll}E\left( Y^2\rp&\dsp=\int_{-\infty}^{+\infty}x^2g(x)dx\\[1.3em]
&\dsp=2\int_{-\infty}^{+\infty}x^2\varphi(x)\Phi(x)dx\\[1.3em]
&\dsp=2\int_{+\infty}^{-\infty}(-u)^2\varphi(-u)\Phi(-u)\lp-du\rp\\[1.3em]
&\dsp=2\int_{-\infty}^{+\infty}u^2\varphi(u)\lp1-\Phi(u)\right) du\\[1.3em]
&=2E\left( X^2\rp-E\left( Y^2\rp\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/49.png)
or
![\[\begin{array}{ll}V\left( X^2\rp=1&=E\left( X^2\rp-\left( E(X)\rp^2=E\left( X^2\rp-0\\[1em]
&\iff E\left( X^2\rp=1\enar\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/50.png)
et alors
![\[E\left( Y^2\rp=2-E\left( Y^2\rp\iff
E\left( Y^2\rp=1\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/51.png)
et donc, finalement,
![\[V(Y)=1-\dfrac1\pi\]](/Generateur-Devoirs/Colles/VAC/Loi-normale-produit-densite-repartition_c/52.png)
- On a