🔍

Colles de mathématiques

Racine carrée d'une loi exponentielle


Sujet


Soit $\lambda>0$ et
\[f:\R\to\R, \, x\mapsto\la\begin{array}{cl} 0 &\text{si } x\leqslant0 \\ \lambda e^{-\lambda x} &\text{sinon}\enar\right.\]


  1. Vérifier que $f$ est une densité de probabailité d'une variable aléatoire.
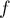    Soit $X$ admettant $f$ pour densité.
  2. Montrer que 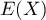$E(X)$ et $V(X)$ existent et les calculer.
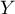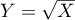  3. On définit $Y$ par $Y=\sqrt{X}$. Déterminer une densité de $Y$.
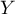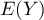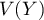  4. Montrer que $E(Y)$ et $V(Y)$ existent et les calculer.

Corrigé de l'exercice de maths: Variables aléatoires continues

Correction


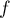  1. $f$ est clairement positive et continue, sauf en 0, et
    \[\begin{array}{ll}\dsp\int_{-\infty}^{+\infty}f(x)dx &=\dsp\lambda\int_0^{+\infty}e^{-\lambda x}dx\\ &=\lambda\left[ -\dfrac1\lambda e^{-\lambda x}\rb_0^{+\infty} =1\enar\]

    ce qui finit de montrer que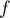 $f$ est une densité de variable aléatoire.

  2. \[E(X)=\lambda\int_0^{+\infty}xe^{-\lambda x}dx\]

    Comme
    \[\dsp\lim_{x\to+\infty}x^2\left( xe^{-\lambda x}\rp=0\]

    et d'après le critère de Riemann, cette intégrale converge bien en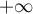 $+\infty$, et, en intégrant par parties,
    \[\begin{array}{ll}E(X)&=\dsp\lambda\lb-\dfrac{x}\lambda e^{-\lambda x}\rb_0^{+\infty} +\int_0^{+\infty}e^{-\lambda x}dx\\ &=0+\lb-\dfrac1\lambda e^{-\lambda x}\rb_0^{+\infty}\\ &=\dfrac1\lambda\enar\]

    et de même (ou en ayant reconnu la loi exponentielle)
    \[V(X)=\dfrac1{\lambda^2}\]



  3. \[\begin{array}{ll}F_Y(x)&=P(Y\leqslant x)\\ &=P\lp\sqrt{X}\leqslant x\rp\\ &=P\left( X\leqslant x^2\rp\\ &=F_X\left( x^2\rp\enar\]

    d'où
    \[F_Y(x)=\la\begin{array}{cl}0&\text{si} x\leqslant0\\ F_X\left( x^2\rp=&\text{sinon}\enar\right.\]

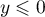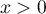    et donc, la densité, $f_Y(x)=0$ pour $y\leqslant0$ et, pour $x>0$ en dérivant
    \[f_Y(x)=2\lambda xF'_X(x^2)=2xe^{-\lambda x^2}\]


  4. \[E(Y)=\int_{-\infty}^{+\infty}yf_Y(y)dy =2\lambda \int_0^{+\infty}y^2e^{-\lambda y^2}dy\]

    et, en intégrant par parties
    \[\begin{array}{ll}\dsp\int_0^{+\infty}&y^2e^{-\lambda y^2}dy =\dsp\int_0^{+\infty} y\times y e^{-\lambda y^2}dy\\[1em] &=\dsp\left[ y\tm\dfrac{-1}{2\lambda} e^{-\lambda y^2}\rb_0^{+\infty} +\dfrac1{2\lambda}\int_0^{+\infty} e^{-\lambda y^2}dy \enar\]

    La partie intégrée est nulle, et la dernière intégrale se calcule en se ramenant à la loi normale, en posant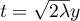 $t=\sqrt{2\lambda}y$, soit
    \[\int_0^{+\infty}e^{-\lambda y^2}dy =\dfrac1{\sqrt{2\lambda}}\int_0^{+\infty} e^{-t^2/2}dt\]

    car pour $Z$ qui suit la loi normale centrée réduite,
    \[\begin{array}{ll}&P(Z\geqslant0)=\dsp\int_0^{+\infty}\dfrac1{\sqrt{2\pi}}e^{-t^2/2}dt =\dfrac12\\ &\implies\displaystyle \int_0^{+\infty}e^{-t^2/2}dt =\dfrac{\sqrt{2\pi}}2=\sqrt{\dfrac\pi2} \enar\]

    d'où
    \[E(Y)=2\lambda\int_0^{+\infty}y^2e^{-\lambda y^2}dy =\dfrac1{\sqrt{2\lambda}}\sqrt{\dfrac\pi2} =\dfrac12\sqrt{\dfrac\pi\lambda} \]

    On a ensuite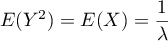 $E(Y^2)=E(X)=\dfrac1\lambda$, et donc
    \[V(Y)=E\left( Y^2\rp-\left( E(Y)\rp^2=\dfrac1\lambda-\dfrac\pi{4\lambda} =\dfrac{4-\pi}{4\lambda}\]