🔍

Colles de mathématiques

Réciproque d'une fonction de répartition

Oral ESCP - filière B/L, 2021


Sujet


Oral ESCP, BL - 2021
Soit f la fonction définie sur R par, pour tout réel x,
f (x) = 2/(ex + e−x)2
  1. Montrer que f peut être considérée comme une densité d'une certaine variable aléatoire X.
    1. Montrer que X possède une espérance et donner sa valeur.
    2. Montrer que X possède une variance (on ne demande pas sa valeur).
    3. On note F la fonction de répartition de X. Montrer, sans calculer F(x), que F est une bijection de R dans un intervalle I que l’on précisera.
  3. On considère la variable aléatoire Y définie par Y = F(X).
    1. Déterminer la loi de Y.
    2. Calculer l'expression de F(x) pour tout réel x.
    3. Déterminer F−1, bijection réciproque de F.

Corrigé de l'exercice de maths: Variables aléatoires continues - Annales ESCP - B/L

Correction


Oral ESCP, BL - 2021
  1. f est clairement positive et continue sur R. De plus, pour A>0,
    \[\begin{array}{ll}\dsp\int_{-A}^A f(x)dx &=\dsp\int_{-A}^A\dfrac2{\left( e^x+e^{-x}\rp^2}dx\\ &=\dsp\int_{-A}^A\dfrac{2e^{2x}}{e^{2x}\left( e^x+e^{-x}\rp^2}dx\\ &=\dsp\int_{-A}^A\dfrac{2e^{2x}}{\left( e^{2x}+1\rp^2}dx\\ &=\lb\dfrac{-1}{e^{2x}+1}\rb_{-A}^A\\ &=-\dfrac1{e^{2A}+1}+\dfrac1{e^{-2A}+1} \enar\]

    et on trouve donc, à la limite où A+∞,
    \[\int_{-\infty}^{+\infty}f(t)dt=1\]

    ce qui finit de montrer que f peut bien être considérée comme une densité de probabilité.
  2. On a t2(t f (t))0 lorsque t+∞, par croissances comparées, ce qui montre, par comparaison avec une intégrale de Riemann, que t ↦ t f(t) est intégrable en l'infini, et donc que E(X) existe.
    De plus, comme f est paire, on en déduit que t ↦ t f(t) est impaire, et alors que E(X) = 0.
  3. De même que précédemment, t2(t2f (t))0 lorsque t+∞ et donc X admet aussi un moment d'ordre 2 (et des moments de tout ordre, de la même façon), et en particulier, V(X) existe.
  4. On sait que F est une fonction continue, strictement croissante sur R avec
    \[\lim_{x\to-\infty}F(x)=0\]

    et
    \[\lim_{x\to+\infty}F(x)=1\]

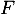    et ainsi, $F$ est une bijection de R dans ]0; 1[.
    (et ceci est vrai pour tout fonction de répartition).
    1. On a Y(Ω) = ]0; 1[. On s'intéresse à la fonction de répartition de Y, pour x∈]0; 1[,
      \[F_Y(x)=P(Y\leqslant x) =P(F(X)\leqslant x)\]

      Comme, d'après la question précédente, F est bijective, on peut utiliser sa réciproque F−1, et alors
      \[F_Y(x)=P(X\leqslant F^{-1}(x))\]

      et donc, en revenant à la fonction de répartition de X,
      \[F_Y(x)=F\left( F^{-1}(x)\rp=x\]

      On en déduit que la densité de Y est constante sur ]0; 1[: il s'agit de la loi uniforme.
    2. On a déjà vu le calcul à la première question:
      \[\begin{array}{ll}F(x)&=\dsp\int_{-\infty}^xf(t)dt\\ &=\lb\dfrac{-1}{e^{2x}+1}\rb_{-\infty}^x\\ &=1-\dfrac1{e^{2x}+1} \enar\]


    3. Pour déterminer l'expression de la fonction réciproque, on cherche à inverser la relation F(x) = y
      \[\begin{array}{rl}F(x)&=1-\dfrac1{e^{2x}+1}=y\\ \iff&\dfrac1{e^{2x}+1}=1-y\\ \iff&e{2x}+1=\dfrac1{1-y}\\ \iff&e{2x}=\dfrac1{1-y}-1=\dfrac{y}{1-y}\\ \iff&2x=\ln\lp\dfrac{y}{1-y}\rp\\ \iff&x=F^{-1}(y)=\dfrac12\ln\lp\dfrac{y}{1-y}\right) \enar\]