Colles de mathématiques
Somme directe des espaces vectoriels des matrices symétriques et antisymétiques, et diagonalisation d'une application
Sujet
On considère l'application:
Φ:
ℳn(R)
ℳn(R)
A
↦
A − AT
On note de plus 𝒮n(R) et 𝒜n(R) les ensembles des matrices symétriques et antisymétriques.
On note de plus 𝒮n(R) et 𝒜n(R) les ensembles des matrices symétriques et antisymétriques.
- Montrer que Φ est un endomorphisme de ℳn(R).
- Déterminer Ker(Φ) et montrer que Im(Φ) = 𝒜n(R).
- Montrer que ℳn(R) = 𝒜n(R)⊕𝒮n(R).
- Montrer que les seules valeurs propres de Φ sont 0 et 2.
- Montrer que Φ est diagonalisable.
Corrigé de l'exercice de maths: Matrices - Diagonalisation
Correction
- Par linéarité de la soustraction matricielle et de la transposition,
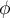 est bien linéaire de
est bien linéaire de
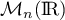 dans
dans 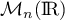 ,
et c'est donc bien un endomorphisme de
,
et c'est donc bien un endomorphisme de 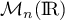 .
.
-
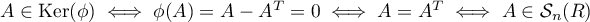 .
.
Ainsi,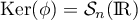 .
.
Soit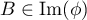 ,
alors il existe
,
alors il existe 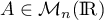 tel que
tel que
 .
On a alors
.
On a alors 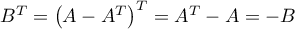 et donc
et donc
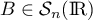 ,
d'où
,
d'où 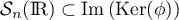 Réciproquement,
si
Réciproquement,
si 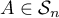 ,
alors
,
alors 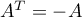 et alors
et alors 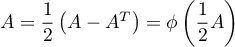 ,
ce qui montre que
,
ce qui montre que 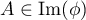 et donc
que
et donc
que 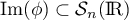 .
.
On vient ainsi de montrer que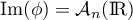 .
.
- La somme est directe, car si
 ,
alors
,
alors 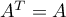 et
et 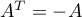 d'où
d'où 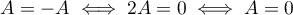 .
.
De plus, pour toute matrice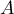 , on peut écrire
, on peut écrire
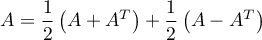 avec
avec 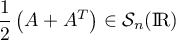 et
et 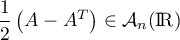 , ce qui
montre que
, ce qui
montre que
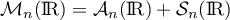 .
.
Comme la somme est directe on a donc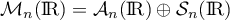 .
.
- Soit
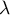 une valeur propre de
une valeur propre de 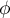 et
et
 une matrice propre, c'est-à-dire
une matrice propre, c'est-à-dire
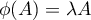 .
En particulier, si
.
En particulier, si 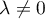 ,
,
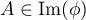 et donc,
d'après ce qui précède,
et donc,
d'après ce qui précède,
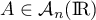 , d'où
, d'où
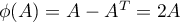 et nécessairement, si
et nécessairement, si 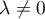 ,
alors
,
alors 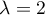 .
.
Par ailleurs,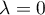 est aussi valeur propre car on a vu que
est aussi valeur propre car on a vu que
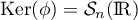 .
.
- On a
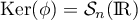 et donc
et donc
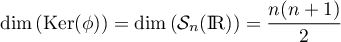 .
De même,
.
De même,
 .
Au total, on a deux valeurs propres, pour lesquelles la somme des dimensions des espaces propres est
.
Au total, on a deux valeurs propres, pour lesquelles la somme des dimensions des espaces propres est
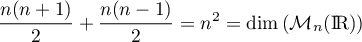 ,
et donc
,
et donc 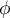 est diagonalisable.
est diagonalisable.