Colles de mathématiques
Sous-espaces vectoriels
Sujet
Déterminer lesquels des ensembles
E1,
E2 et
E3
sont des sous-espaces vectoriels de
R3:
- E1 = {(x, y, z) ∈ R3 ; x+2y = z}
- E2 = {(x, y, z) ∈ R3 ; x2+y2+z2 = 1}
- E3 = {(x, y, z) ∈ R3 ; x(y+z) = 0}
Corrigé de l'exercice de maths: Espaces vectoriels
Correction
- E1 est un sous-espace vectoriel:
 ,
et si
,
et si 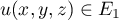 et
et 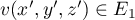 et
et  ,
donc
,
donc 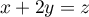 et
et 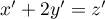 et
alors
et
alors 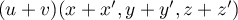 avec
avec
![\[(x+x')+2(y+y')=\left( x+2y\rp+\left( x'+2y'\rp
=z+z'\]](/Generateur-Devoirs/Colles/ev/exsev_c/9.png)
et donc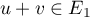 .
De même,
.
De même, 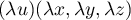 avec
avec
![\[\lambda x+2(\lambda y)
=\lambda(x+2y)
=\lambda z\]](/Generateur-Devoirs/Colles/ev/exsev_c/12.png)
et donc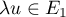 .
Ainsi, E1 est un sous-espace vectoriel de R3.
.
Ainsi, E1 est un sous-espace vectoriel de R3.
- E2 n'est pas un espace vectoriel.
Il suffit de trouver un contre exemple, par exemple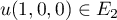 , mais
, mais 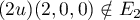 .
.
- De même, E3 n'est pas un espace vectoriel.
Il suffit de trouver un contre exemple, par exemple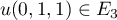 et
et  ,
mais
,
mais 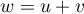 tel que
tel que
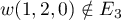 .
.