🔍

Colles de mathématiques

Comportement asymptotique de l'espérance du max de lois exponentielles

Oral ENS Ulm, filière B/L, 2017


Sujet


Soit 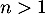$n>1$ un entier et $(X_i)$ des variables aléatoires indépendantes de même loi exponentielle de paramètre 1. On pose:
\[M_n = \max\left( X_1 , \dots , X_n\rp\]

  1. Montrer que 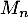$M_n$ admet une densité, qu'on déterminera et qu'on représentera graphiquement.
  2. Montrer que l’intégrale 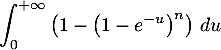$\dsp\int_0^{+\infty} \left( 1-\left(1-e^{-u}\rp^n\rp\,du$ converge.
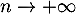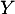  3. Déterminer la valeur de la limite de $\dfrac{E\left[ M_n\right]}{\ln(n)}$ quand $n\to+\infty$. Indication : on pourra utiliser, sans preuve, le fait que $E[Y]=\dsp\int_0^{+\infty}P(Y\geqslant u)\,du$ pour toute variable aléatoire positive $Y$ faire un changement de variable dans l’intégrale.

Corrigé de l'exercice de maths: Variables aléatoires continues - Annales ENS Ulm - B/L

Correction


Oral ENS ULM - 2017

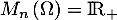  1. On a $X_i\lp\Omega\rp=\R_+$ donc aussi $M_n\lp\Omega\rp=\R_+$.
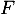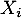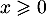    On note $F$ la fonction de répartition des $X_i$, donc $F(x)=1-e^{-x}$ si $x\geqslant0$ et 0 sinon, et on note de même $F_n$ la fonction de répartition de $M_n$.

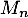    On a alors pour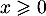 $x\geqslant0$, et par indépendance des variables aléatoires,
    \[\begin{array}{lcl} F_n(x)&=&P\left( M_n\leqslant x\rp\\[.5em] &=&P\left( \max(X_1,\dots,X_n)\leqslant x\rp\\[.5em] &=&P\biggl( \left( X_1\leqslant x\rp\cap\dots\cap\left( X_1\leqslant x\rp\biggr)\\ &=&\dsp\prod_{i=1}^nP\left( X_i\leqslant x\rp\\[1.5em] &=&\left( F(x)\rp^n = \lp1-e^{-x}\rp^n\enar\]

    tandis que
    \[F_n(x)=P\left( M_n\leqslant x\rp=0 \text{ pour } x<0\]

    La fonction de densité est alors donnée par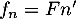 $f_n=Fn'$, soit pour $n=1$,
    \[f_1(x)=\la\begin{array}{ll}0 &\text{ si } x<0\\e^{-x}&\text{ si } x\geqslant0\enar\right.\]

    et la courbe
    \[\psset{yunit=2cm,arrowsize=8pt}\begin{pspicture}(-5,-.5)(6,1.4) \psline{->}(-5,0)(6,0) \psline{->}(0,-.2)(0,1.4) \psline[linecolor=blue,linewidth=1.5pt](-5,0)(0,0) \psplot[linecolor=blue,linewidth=1.5pt]{0}{5}{2.718 x -1 mul exp} \psline(-.1,1)(.1,1)\rput[r](-.2,1){1} \end{pspicture}\]

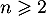    Pour $n\geqslant2$, on a
    \[f_n(x)=\la\begin{array}{ll}0 &\text{ si } x<0\\ ne^{-x}\lp1-e^{-x}\rp^{n-1}&\text{ si } x\geqslant0\enar\right.\]

    et donc, pour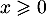 $x\geqslant0$,
    \[\begin{array}{lcl} f_n'(x)&=&ne^{-x}\lp1-e^{-x}\rp^{n-2}\biggl(-\lp1-e^{-x}\rp+(n-1)e^{-x} \biggr)\\[1em] &=&ne^{-x}\lp1-e^{-x}\rp^{n-2}\biggl(-1+ne^{-x}\biggr) \enar\]

    et la fonction est donc croissante puis décroissante, avec un maximum en $x_n$ tel que
    \[-1+ne^{-x}=0 \iff x=\ln(n)\]

    et on obtient l'allure de la courbe
    \[\psset{xunit=1cm,yunit=3cm,arrowsize=8pt}\begin{pspicture}(-5,-.5)(6,1.2) \newcommand{\f}[2]{2.718 #1 -1 mul exp #2 mul 1 2.718 -1 #1 mul exp sub #2 1 sub exp mul } \psline{->}(-.2,0)(6,0) \psline{->}(0,-.2)(0,1.2) \psline[linecolor=blue,linewidth=1.5pt](-5,0)(0,0) \psplot[linecolor=blue,linewidth=1.5pt]{0}{5}{\f{x}{2}} \psline(-.1,1)(.1,1)\rput[r](-.2,1){1} \psline(.69,0)(!.69\space\f{.69}{2})(!0\space\f{.69}{2})\rput(.69,-.1){\blue$\ln2$} %n=5 et ln(5)~1.61 \psline[linecolor=red,linewidth=1.2pt](-5,0.01)(0,0.01) \psplot[linecolor=red,linewidth=1.5pt]{0}{5}{\f{x}{5}} \psline(1.61,0)(!1.61\space\f{1.61}{5})(!0\space\f{1.61}{5})\rput(1.61,-.1){\red$\ln5$} \rput(.7,.6){\blue$n\!=\!2$} \rput(4.2,.2){\red$n\!=5\!$} \end{pspicture}\]

  2. La fonction à intégrer est continue sur 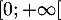$[0;+\infty[$, et seule la convergence en l'infini est donc éventuellement problématique.
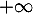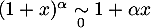    En $+\infty$ on a $e^{-u}\to0$ et l'équivalent $(1+x)^\alpha\underset{0}{\sim}1+\alpha x$ donne alors
    \[1-\lp1-e^{-u}\rp^n\underset{0}{\sim}ne^{-u}\]

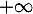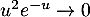    qui est intégrable en $+\infty$, par exemple par critère de Riemann car $u^2e^{-u}\to0$ par croissances comparées.
    L'intégrale converge donc bien.
  3. En utilisant la formuel de l'énoncé, on a
    \[\begin{array}{lcl} E\left[ M_n\rp&=&\dsp\int_0^{+\infty}P\left( M_n\geqslant u\rp\,du\\[1em] &=&\dsp\int_0^{+\infty}\left( 1-P\left( M_n< u\rp\rp\,du\\[1em] &=&\dsp\int_0^{+\infty}\left( 1-\left(1-e^{-u}\rp^n\rp\,du \enar\]

    qui est l'intégrale convergente de la question précédente.

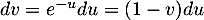    On effectue le changement de variable $v=1-e^{-u}$, avec $dv=e^{-u}du=(1-v)du$ et alors
    \[\int_0^{+\infty}\left( 1-\left(1-e^{-u}\rp^n\rp\,du =\int_0^1\dfrac{1-v^n}{1-v}\,dv\]

    Le terme à intégrer est la somme des termes d'une suite géométrique:
    \[\dfrac{1-v^n}{1-v}=\sum_{k=0}^{n-1}v^k\]

    et donc, par linéarité de l'intégrale,
    \[\begin{array}{lcl} E\left[ M_n\right] &=&\dsp\int_0^{+\infty}\left( 1-\left(1-e^{-u}\rp^n\rp\,du\\[1.2em] &=&\dsp\sum_{k=0}^{n-1}\int_0^1v^k\,dv\\[1.2em] &=&\dsp\sum_{k=0}^{n-1}\dfrac1{k+1}\\[1.2em] &=&\dsp\sum_{k=1}^n\dfrac1k \enar\]

    qui est la somme partielle de la série harmonique donc on sait qu'elle diverge vers $+\infty$ avec, plus précisément
    \[\sum_{k=1}^n\dfrac1k\underset{+\infty}{\sim}\ln(n)\]

    On trouve donc finalement que
    \[\lim_{n\to+\infty}\dfrac{E\left[ M_n\right]}{\ln(n)}=1\]




    Remarque: À savoir démontrer (question bonus ?): la formule donnée dans l'énoncé pour le calcul de l'espérance, et l'équivalent pour la série harmonique.
    • Formule pour l'espérance
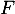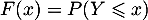      Soit $Y$ une variable aléatoire sur $\R_+$, de densité $f$ et de fonction de répartition $F$ définie par $F(x)=P(Y\leqslant x)$.
      Comme le suggère la formule souhaitée, on passe par l'événement contraire en posant
      \[G(x)=P(Y>x)=1-F(x)\]

      On a alors,
      \[\begin{array}{lcl}E[Y]&=&\dsp\int_0^{+\infty}xf(x)\,dx\\ &&=\dsp\int_0^{+\infty}xF'(x)\,dx\\ &&=\dsp-\int_0^{+\infty}xG'(x)\,dx\\ \enar\]

      puis, en intégrant par parties,
      \[\begin{array}{lcl}E[Y]&=&-\bigl[\,xG(x)\,\bigr]_0^{+\infty}+\dsp\int_0^{+\infty}G(x)\,dx\\[1em] &=&\dsp\int_0^{+\infty}P(Y>x)\,dx\enar\]

      bien sûr sous réserve que les intégrales considérées convergent et que
      \[\lim_{x\to+\infty}xG(x)=0\]

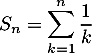
    • Équivalent de la série harmonique $S_n=\dsp\sum_{k=1}^n\dfrac1k$
      On utilise la comparaison série-intégrale: comme $t\mapsto\dfrac1t$ est décroissante, on a
      \[k\leqslant t\leqslant k+1 \iff \dfrac1{k+1}\leqslant\dfrac1t\leqslant\dfrac1k\]

      puis en intégrant,
      \[\dfrac1{k+1}\leqslant\int_k^{k+1}\dfrac1t\,dt\leqslant\dfrac1k\]

      et enfin en sommant,
      \[\sum_{k=1}^n\dfrac1{k+1} \leqslant\sum_{k=1}^n\int_k^{k+1}\dfrac1t\,dt \leqslant\sum_{k=1}^n\dfrac1k\]

      soit,
      \[S_{n+1}\leqslant\int_1^{n+1}\dfrac{dt}{t}=\ln(n+1)\leqslant S_n\]

      On a donc obtenu que
      \[S_{n+1}\leqslant\ln(n+1)\]

      soit aussi
      \[S_n\leqslant\ln(n)\]

      et que
      \[S_n\geqslant\ln(n+1)\]

      soit, en résumé,
      \[\ln(n+1)\leqslant S_n\leqslant\ln(n)\]

      et donc,
      \[\dfrac{\ln(n+1)}{\ln(n)}\leqslant\dfrac{S_n}{\ln(n)}\leqslant1\]

      et on obtient la limite et l'équivalent grâce au théorème des gendarmes.