Colles de mathématiques
Espérance et fonction de répartition
Oral ENSAE, Saclay, filière B/L, 2019
Exercice de maths: Variables aléatoires continues - Annales ENSAE - Saclay - B/L
Sujet
Soit 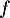 une densité de probabilité d'une variable aléatoire
une densité de probabilité d'une variable aléatoire 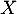 à valeurs dans
à valeurs dans 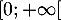 , et
, et 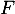 sa fonction de répartition.
On note:
sa fonction de répartition.
On note:
![\[\forall t\geqslant0,\ Q(t) =1-F(t)\]](/Generateur-Devoirs/Colles/VAC/Efp/5.png)
On suppose qu'il existe tel que
tel que
![\[\lim_{t\to+\infty}t^\alpha Q(t)=0\]](/Generateur-Devoirs/Colles/VAC/Efp/7.png)
On suppose qu'il existe
- Montrer que
![$E[X]$](/Generateur-Devoirs/Colles/VAC/Efp/8.png) existe et que
existe et que
![\[E[X]=\int_0^{+\infty}Q(t)\,dt\]](/Generateur-Devoirs/Colles/VAC/Efp/9.png)
- Soit
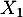 , … ,
, … , 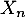 ,
, 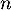 variables aléatoires indépendantes,
toutes de loi exponentielle de paramètre 1.
variables aléatoires indépendantes,
toutes de loi exponentielle de paramètre 1.
On note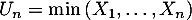 .
.
Déterminer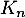 la fonction de répartition de
la fonction de répartition de 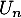 .
.
En déduire l'espérance et la variance de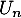 .
.
- Soit
 qui suit une loi géométrique de paramètre
qui suit une loi géométrique de paramètre ![$p\in]0, 1[$](/Generateur-Devoirs/Colles/VAC/Efp/18.png) .
On note
.
On note 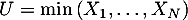 .
.
Déterminer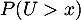 pour tout
pour tout  .
.
La variable aléatoire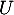 admet-elle une espérance ? Si oui, la calculer.
admet-elle une espérance ? Si oui, la calculer.