Colles de mathématiques
Étude de deux sous-espaces vectoriels, dimensions, intersection, supplémentaires
Retour
Sujet
Soit F et G les sous-espaces vectoriels de R3 définis par:
F =
{(x, y, z) ∈ R3 ;
x − 2y + z = 0}
et
G =
{(x, y, z) ∈ R3 ;
2x − y + 2z = 0}
- Donner une base de F, une base de G, en déduire leur dimension respective.
- Donner une base de F∩G, et donner sa dimension.
- Montrer que la famille constituée des vecteurs de la base de F et des vecteurs de la base de G trouvées en a) est une famille génératrice de R3.
Est-elle libre? - Les espaces F et G sont-ils supplémentaires?
Corrigé de l'exercice de maths: Espaces vectoriels
Correction
- On trouve d'abord une famille génératrice de
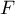 . On a :
. On a :
![\[\begin{array}{ll}(x,y,z)\in F&\iff x-2y+z=0\\[.4em]
&\iff\la\begin{array}{rcccc}
x&=&y\times 2&+&z\times(-1)\\
y&=&y\times 1&+&z\times 0\\
z&=&y\times 0&+&z\times 1.
\enar\right.\enar\]](/Generateur-Devoirs/Colles/ev/exsevsup3_c/2.png)
et ainsi, les vecteurs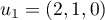 et
et 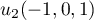 engendrent
engendrent 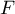 . De plus, ces deux vecteurs ne sont pas colinéaires, et
donc la famille est libre: c'est donc une base de
. De plus, ces deux vecteurs ne sont pas colinéaires, et
donc la famille est libre: c'est donc une base de  qui est de dimension 2.
qui est de dimension 2.
On procède de même pour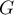 :
:
![\[\begin{array}{ll}
(x,y,z)\in F&\iff 2x-y+2z=0\\[.4em]
&\iff\la\begin{array}{rcccc}
x&=&x\times 1&+&z\times0\\
y&=&x\times 2&+&z\times2\\
z&=&x\times 0&+&z\times1.
\enar\right.
\enar\]](/Generateur-Devoirs/Colles/ev/exsevsup3_c/8.png)
On trouve cette fois que les vecteurs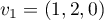 et
et  forment une base de
forment une base de 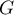 qui est aussi de dimension 2.
qui est aussi de dimension 2.
- On a, pour cette intersection:
![\[\begin{array}{ll}(x,y,z)\in F\cap G
&\iff\la\begin{array}{rcl}
x-2y+z&=&0\\
2x-y+2z&=&0\\
\enar\right.\\[1.6em]
&\iff\la\begin{array}{rcl}
x-2y+z&=&0\\
3y&=&0\\
z&=&z\\
\end{array}\right.\\[2em]
&\iff\la\begin{array}{rcl}
x&=&z\times(-1)\\
y&=&z\times 0\\
z&=&z\times 1
\enar\right.\enar\]](/Generateur-Devoirs/Colles/ev/exsevsup3_c/12.png)
et ainsi le vecteur engendre cette intersection. Ce vecteur étant non-nul, il constitue une base de
engendre cette intersection. Ce vecteur étant non-nul, il constitue une base de 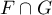 qui est donc, en particulier, de dimension 1.
qui est donc, en particulier, de dimension 1.
- Il s'agit de montrer que
 est une famille génératrice de
est une famille génératrice de 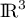 .
.
Méthode 1. Pour on cherche à écrire
on cherche à écrire
![\[\begin{array}{lcl}&&(x,y,z)=au_1+bu_2+cv_1+dv_2\\[.4em]
&\iff&\la\begin{array}{rcl}
2a-b+c&=&x\\
a+2c+2d&=&y\\
b+d&=&z\\\enar\right.\\[1.6em]
&\iff&\la\begin{array}{rcl}
2a-b+c&=&x\\
b+3c+4d&=&2y-x\\
b+d&=&z\enar\right.\\[1.6em]
&\iff&\la\begin{array}{rcl}
2a-b+c&=&x\\
b+3c+4d&=&2y-x\\
3c+3d&=&2y-x-z.\enar\right.
\enar\]](/Generateur-Devoirs/Colles/ev/exsevsup3_c/18.png)
On voit donc qu'on peut imposer une valeur quelconque à , puis, le système étant triangulaire, obtenir la valeur de
, puis, le système étant triangulaire, obtenir la valeur de  grâce à la 3ème équation, puis celle de
grâce à la 3ème équation, puis celle de  par la 2ème équation et enfin celle
par la 2ème équation et enfin celle 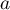 avec la 1ère équation.
avec la 1ère équation.
Méthode 2. L'espace vectoriel engendré par la réunion des deux bases est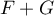 . On doit démontrer que
. On doit démontrer que 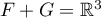 , et
pour cela il suffit de démontrer que
, et
pour cela il suffit de démontrer que  .
La formule de Grassmann s'écrit
.
La formule de Grassmann s'écrit
![\[\dim(F+G)=\dim(F)+\dim(G)-\dim(F\cap G)=2+2-1=3\]](/Generateur-Devoirs/Colles/ev/exsevsup3_c/26.png)
ce qu'il fallait démontrer.
Cette famille n'est de plus pas libre car une famille libre de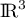 a au plus trois éléments.
a au plus trois éléments.
-
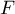 et
et 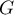 ne sont pas supplémentaires car
ne sont pas supplémentaires car 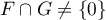 .
.