🔍

Colles de mathématiques

Lois de Pareto et exponentielle

Oral ENSAE, Saclay, filière B/L, 2019



Exercice de maths: Variables aléatoires continues - Annales ENSAE - Saclay - B/L

Sujet


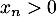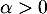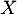Soit $x_n>0$ et soit $\alpha>0$. On définit $X$ une variable aléatoire telle que:
\[\forall x\in\R, \ P(X>x)=\la\begin{array}{cl}\lp\dfrac{x_n}{x}\rp^\alpha &\text{si }\, x\geqslant x_n\\[1em] 1 &\text{sinon}\enar\right.\]

  1. Montrer que 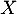$X$ est une variable aléatoire à densité, calculer sa densité.
    Représenter une allure de la fonction de répartition et de la densité.
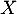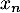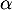    On dit que $X$ suit une loi de Pareto de paramètres $x_n$ et $\alpha$.
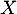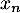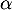  2. Soit $X$ une variable aléatoire qui suit une loi de Pareto de paramètres $x_n$ et $\alpha$.
    Calculer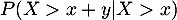 $P(X > x + y | X > x)$.
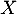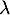    Qu'en est-il si $X$ suit une loi exponentiellle de paramètre $\lambda$ ?
  3. Montrer que :
    \[X \text{ est de loi de Pareto de param\`etres } x_n \text{ et } \alpha \iff \ln\lp\dfrac{X}{x_n}\right) \text{ est de loi } \mathcal{E}(\alpha)\]

  4. À quelles conditions sur 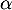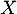$\alpha$, $X$ admet-elle une espérance ?

Correction