🔍

Colles de mathématiques

Racine carrée d'une différence d'exponentielles

Oral HEC - filière B/L, 2022



Exercice de maths: Variables aléatoires continues - Annales HEC - B/L

Sujet


oral HEC, BL - 2022 - Exercice sans préparation.
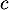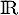Soit $c$ un réel strictement positif. On note $v$ l'application définie sur $\R$ par:
\[v(x)=\la\begin{array}{lll}0&\text{si}&x\leqslant0\\ \dfrac{e^{-c^2x}-e^{-4c^2x}}{x\ln4}&\text{si}&x>0\enar\right.\]


On admet que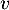 $v$ est une fonction densité de probabilité, et on note 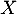$X$ une variable aléatoire de densité $v$.
  1. Montrer que 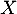$X$ admet une espérance et calculer sa valeur.
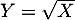  2. On note $Y =\sqrt{X}$. On admet que 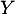$Y$ est une variable à densité.
    Montrer que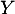 $Y$ admet une espérance et une variance et donner leurs valeurs.

Correction